Модель Вальраса. Модели краткосрочного прогнозирования и регулирования экономики, страница 3

Задачи по курсу «математическая экономика»

1.  Функционал полезности, описывающий валовой внутренний продукт государства, описывается мультипликативной зависимостью:

,

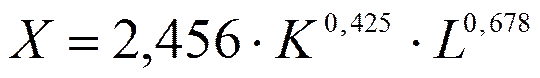известно, что за базовый период ВВП возрос в 3,24 раза, число занятых возросло в 1,45 раза, а основные производственные фонды возросли в 3,18 раза по отношению к базисным показателям. Определить масштаб и эффективность производства, а также частные показатели экономической эффективности.

2.  Модель Леонтьева описывает трехсекторную экономику, состоящую из материального сектора (0), фондосоздающего сектора (1) и потребительского сектора (2). Известны следующие показатели: а_i , i=0,1,2- материалоемкость секторов,  b_i , i=0,1,2 – капиталоемкость секторов. Определить выражения (в общем виде) для матрицы прямых затрат (технологической матрицы) и  матрицы полных затрат.

3.  В условиях задачи 2. рассмотреть дополнительно трудовой сектор (3). Как изменится технологическая матрица , если дополнительно известны с – норма потребления на одного занятого и  l_i>0, i=0,1,2 трудоемкости единиц продукции i-го сектора.

4.   Принимая, что экономика состоит из трех отраслей и описывается технологической матрицей (в относительных показателях):

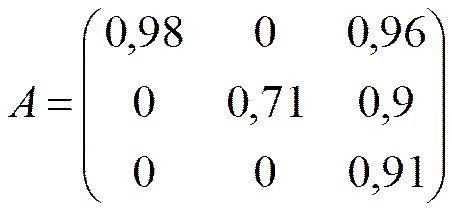
Являются ли отрасли экономики изолированными? Является ли модель Леонтьева для такой экономической системы эффективной?

5.  В модели Солоу, описывающей односекторную систему, заданы внешние показатели:  - годовой темп прироста числа занятых,  - доля выбывших за год основных производственных фондов, a – коэффициент прямых затрат (доля промежуточного продукта в выпуске),  -  норма накопления (доля валовых инвестиций в ВВП) (выбрать самостоятельно, исходя из допустимых значений).

Считая ФП функцией Кобба-Дугласа (α=0.43, А=8.5), составить систему выражений Солоу в абсолютных показателях. Решить задачу максимизации выпуска. Определить, какие еще параметры необходимо задать для получения решения. Дополнить систему, самостоятельно выбрать необходимые параметры.

6.  В условиях задачи 5. сформулировать и решить задачу максимизации среднедушевого потребления.

7.  В модели Неймана матрицы затрат и выпусков имеют вид 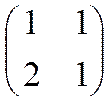 и 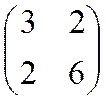 соответственно.  Считая траекторию стационарной, определить значение параметра z.

8.  В условиях задачи 7., считая, что цена изменяется во времени линейно с коэффициентом инфляции (1.05), определить экономическую выгоду. При необходимости, недостающие данные задать самостоятельно.

9.  Определить, какой набор товаров выберет потребитель с доходом 300 у.е., если функция полезности , а цены единицы товаров равны соответственно:

 у.е.,   у.е. у.е.

10.  Предпочтения потребителя заданы функцией:

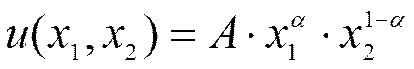
Считая доход потребителя М, а также цены за единицу товаров р₁ и р₂ известными величинами, найти функцию спроса.

11.  В условиях задачи 10 (при α=1/3, А=3, М=100 у.е., р₁=5 у.е. , р₂=10 у.е.) определить максимальную полезность и норму замены второго товара первым.

12.  Производственная функция фирмы имеет вид:

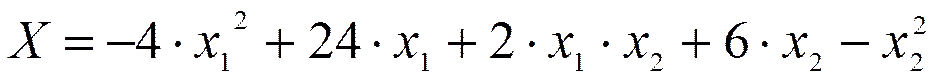,  где  х_1,    х₂   - затраты ресурсов. Определить максимальный выпуск и обеспечивающие этот выпуск ресурсы.

13.  Производственная функция фирмы имеет вид:

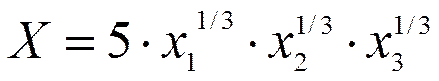 где  х_1,    х_{2  ,}   х ₃- затраты ресурсов.

Определить максимальный выпуск при ограничении на ресурсы:

 

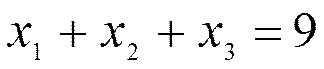
Определить предельные продукты в оптимальной точке.

14.  Прибыли двух конкурирующих фирм на рынке одного товара и цена на этот товар равны соответственно:

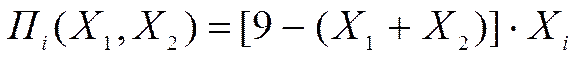, i=1,2 .

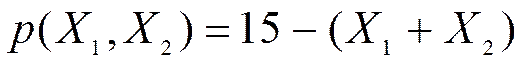, где 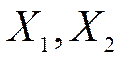 - выпуски фирм.

Определить оптимальные выпуски для каждой фирмы, считая выпуск другой фирмы известной величиной. Сформулировать оптимальный ответ второй фирмы на стратегию первой фирмы, выраженную формулой:

.

15.   Рассмотреть задачу моделирования рыночного торга как задачу моделирования взаимодействия покупателя (потребителя) и продавца (производителя). Определить функции полезности в зависимости от стратегий продавца и покупателя. Считая, что участники сделки заинтересованы в ее заключении,  самостоятельно задать начальные параметры и решить задачу графически с помощью паутинообразной модели. Вывести рекуррентную формулу для автоматизации вычислений.