Изучение имитационного подхода в моделировании на примере системы массового обслуживания – кофейни, страница 6

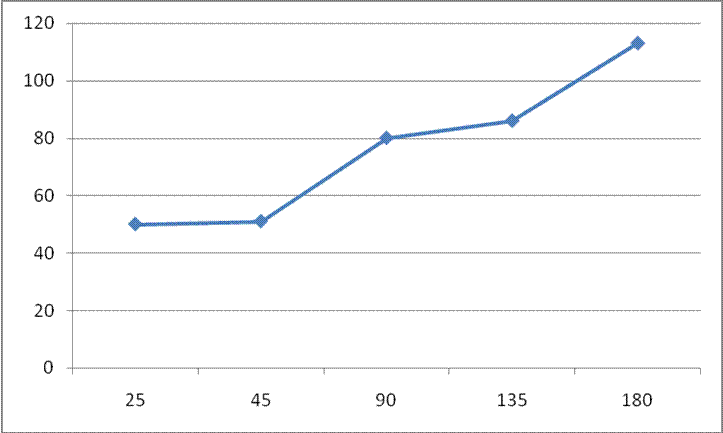
Если попытаться уменьшить время в два раза, за которое буфетчик выполняет заказ, среднее время ожидания выполнения заказа сокращается в два с половиной раза: с 80 до 50.

Так что мы считаем, что следует уделять времени выполнения заказа как можно времени, и тогда посетителей будет больше.

Среднее время ожидания выполнения заказа – Время выполнения заказа  (в секундах).

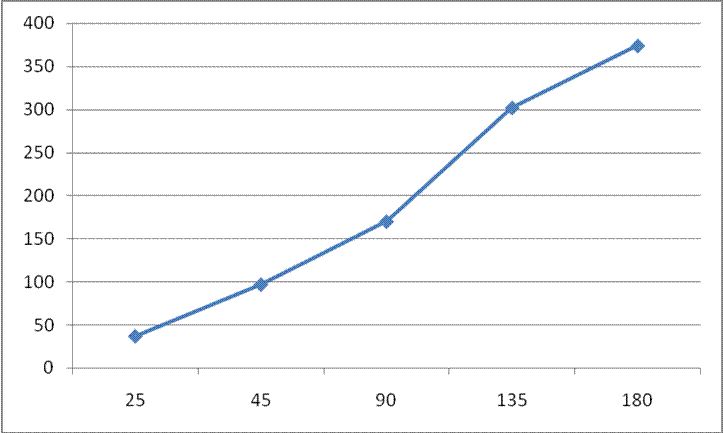
Время простоя кассира – Время выполнения заказа  (в секундах).

3) Изменение параметра «Заявка».

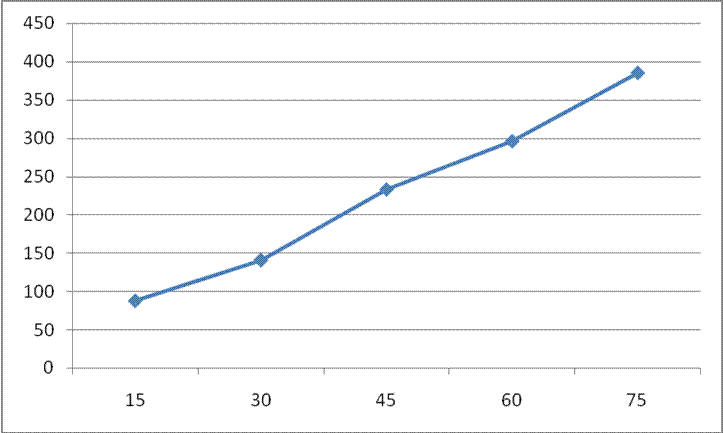
При увеличении этого параметра в два раза время простоя кассира увеличивается с 255 до 499.

Целесообразно вывесить везде ценники, сделать удобную витрину, адекватно читаемые названия блюд, чем короче, тем лучше.

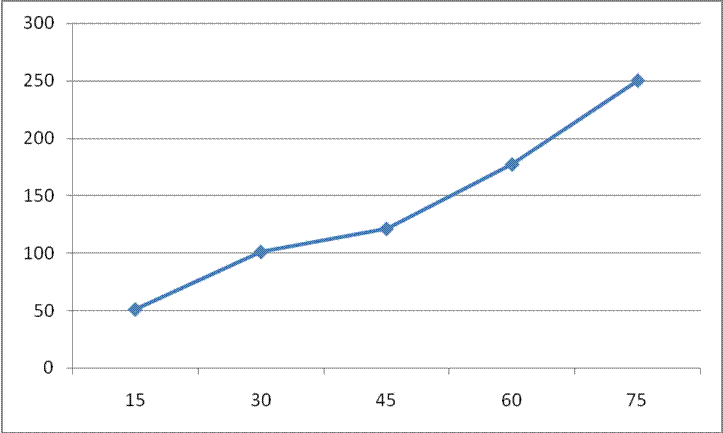
Среднее время ожидания выполнения заказа – Заявка. (в секундах).

Время простоя кассира – Заявка  (в секундах).

Сравнение ручных расчетов и программы (правило подобия).

Ручные расчеты выполнялись простым подсчетом (количество преподавателей, студентов, обслуженных посетителей и отказов).

Среднее время обслуживания = Заявка + Время выполнения заказа + Время расчета. Пример – 7+23+12=42 секунды. Далее полученные различные числа просто складывались и делились на их количество. Таким образом, среднее значение было в пределах от 42 до 57.

Время простоя кассира делалось простым вычитанием из времени моделирования времени работы кассира. В результате получилось: 1800 – 1635 = 165.

Со среднем временем ожидания заказа несколько сложнее, поскольку это были расчеты с заданной точностью – 20%. Для расчета мы взяли диапазон значений времени выполнения заказа. Сначала подсчитываем дисперсию. Для того надо найти сначала среднее значение, что мы и сделали. Получилось число 25,4. Далее необходимо воспользоваться формулой

 ,

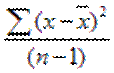где n – размер выборки.  Получаем значение дисперсии, равное 10,3. Далее считаем N по формуле и получаем значение, равное 693. Это будет количество итераций. Проводим расчеты примерно столько раз и получаем сумму средних значений, равную 720,72. Делим эту сумму на N и получаем искомую величину 1,04.

 Тут сравниваются показатели эффективности, рассчитанные вручную и рассчитанные программой – алгоритмом. Как видим, подобие почти полное. Таким образом, можно сказать, что программа работает корректно.

	Ручной расчет	Программа
Общее количество посетителей	35-41	37
Среднее время ожидания выполнения заказа	1,04	1,194
Среднее время обслуживания	42-57	53
Время простоя кассира	165	185,75
Количество отказов	6-7	6
Количество преподавателей	1	1
Количество обслуженных посетителей	29-34	31

Проверка расчетов с заданной точностью (20%).

С заданной точностью мы рассчитывали параметр «Среднее время ожидания выполнения заказа». В результате 7 итераций мы получили 7 различных чисел. Которые вы можете видеть в столбце «Случайные числа». Упорядочиваем их по возрастанию и рассчитываем, на сколько процентов они отличаются. Как видим, разница не больше установленных 20%. Таким образом, расчеты верны.

Случайные числа	Упорядоченные по возрастанию числа
1,101	1,089	99,6%
1,093	1,093		99,9%
1,094	1,094	99,364%
1,089	1,101		99,819%
1,103	1,103	97,01%
1,191	1,137		95,466%
1,137	1,191