Статистика:

И ещё нужно добавить «карман». Он представлен на рисунке ниже. Карман нужен для определения интервалов, по которым мы хотим увидеть статистику.
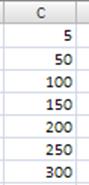
Рис. 1. Карман «Интервала между посещениями».
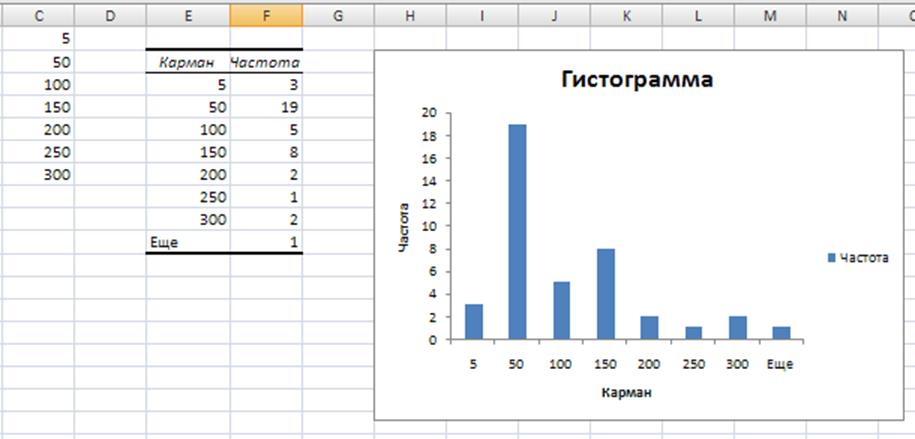
Рис. 2. Результат работы инструмента «Гистограмма» для «Интервала между посещениями».
Для этого воспользуемся формулой: =СУММ((F3-41*1/7))^2/(41*1/7). Запишем ее в ячейку F28. Растянем эту ячейку до F33. Потом рассчитаем сумму.
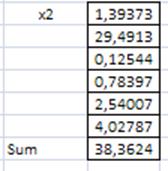
Критерий согласия Пирсона равен 38. Очень плохо. И смотря на график, нельзя сделать какие – либо выводы, поэтому мы отбросили этот способ.
Результата не было. Потом мы поняли, что тут действуют два разных закона. С 13:00 народ идет, потом в 13:30 поток стремительно сокращается и после 13:30 мы видим совсем другой закон. Два закона смешать не получилось, поэтому мы были вынуждены рассчитывать два закона по отдельности. И статистику пришлось снимать заново.
У нас будет два разных закона.
Первый закон действует в момент времени 13:00 – 13:30 (13 часов 00 минут – 13 часов 30 минут).
Статистика:

Тут у нас сложная ситуация. К примеру, заходят два человека. Практически нога в ногу. И как зафиксировать время их прихода? Разве что секундомером, как на Олимпийских играх, где доли секунды имеют решающий фактор. Для удобства мы будем считать двух и более людей, пришедших в один момент времени, как одного человека. Таким образом, из списка исчезнут цифры 1 и 2.
Теперь смотрим:

И ещё нужно добавить «карман». Он представлен на рисунке ниже.
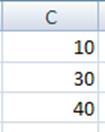
Рис. 3. Карман.
Рис. 4. Анализ данных.
Выбираем пункт «Гистограмма».
Рис. 5. Гистограмма.
Обратите внимание, что нужно пометить галочкой «Вывод графика». А то смотреть будет не на что.
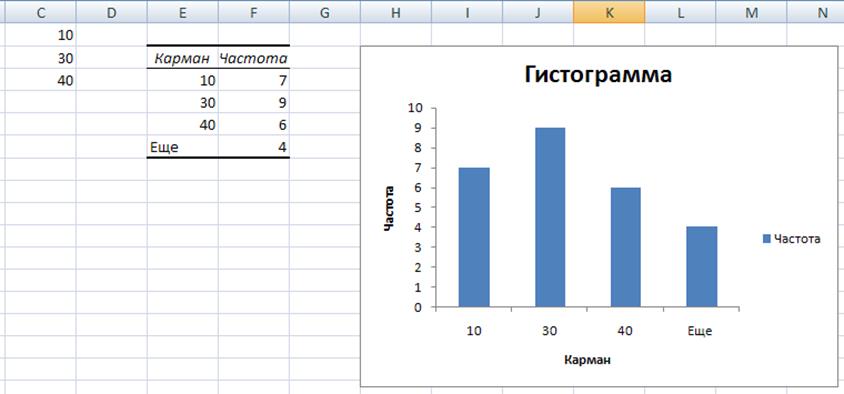
Рис. 6. Результат работы инструмента «Гистограмма».
Для этого воспользуемся формулой: =СУММ((F3-26*1/3))^2/(26*1/3). Запишем ее в ячейку G24. Растянем эту ячейку до G26. Потом рассчитаем сумму.
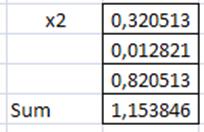
Определяем число степеней свободы v=d-r-1, где d-число интервалов, а r-количество параметров.
V=2. Тогда при 1,15 по таблице распределения Фишера получаем вероятность 0,5. Хорошее значение.
Второй закон действует в момент времени 13:30 – 13:45 (13 часов 30 минут – 13 часов 45 минут). Статистика:
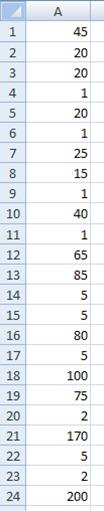
Почему мы убрали 1 и 2 секунды из списка, мы уже описывали выше. Так что комментарии излишни.
Теперь смотрим:
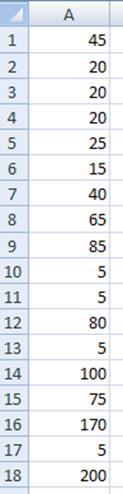
И ещё нужно добавить «карман». Он представлен на рисунке ниже.
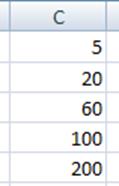
Рис. 7. Карман.

Рис. 8. Анализ данных.
Выбираем пункт «Гистограмма».
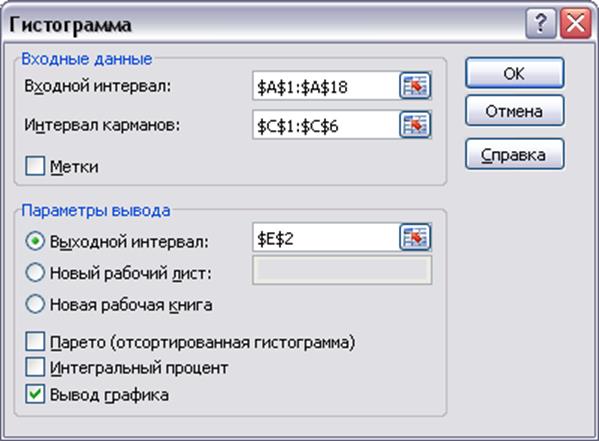
Рис. 9. Гистограмма.
Обратите внимание, что нужно пометить галочкой «Вывод графика».
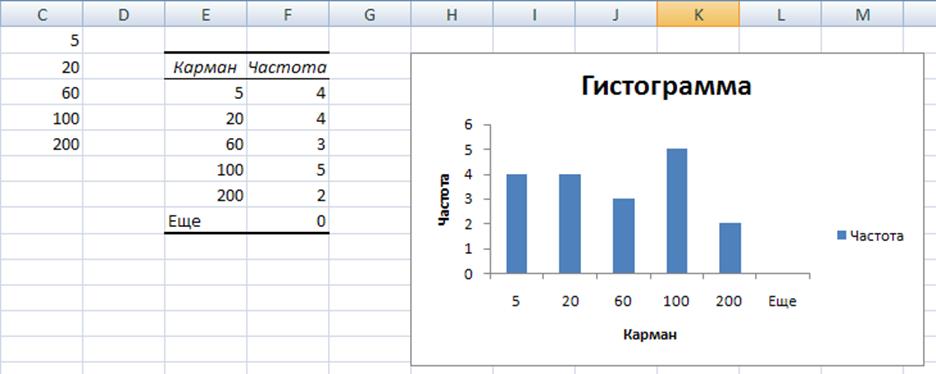
Рис. 10. Результат работы инструмента «Гистограмма».
Для этого воспользуемся формулой: =СУММ((F3-18*1/5))^2/(18*1/5). Запишем ее в ячейку F21. Растянем эту ячейку до F26. Потом рассчитаем сумму.
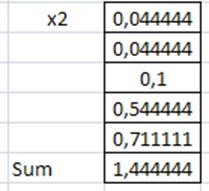
Определяем число степеней свободы v=d-r-1, где d-число интервалов, а r-количество параметров.
V=4. Тогда при 1,44 по таблице распределения Фишера получаем вероятность 0,9. Гипотеза почти верна.
Выбор блюд.
Что такое выбор блюд? Это когда посетитель (страдающий от голода отрок пробегает глазами) просматривает ассортимент доступных блюд и делает выбор. Время пробега глаз посетителя (его голодных глаз) по прилавку кофейни и будем считать за время выбора блюда.

Рис.11. Статистики выбора блюда.
И ещё нужно добавить «карман». Он представлен на рисунке ниже.
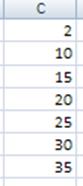
Рис. 12. Карман.
Делаем то же самое, чем мы и занимались наверху.
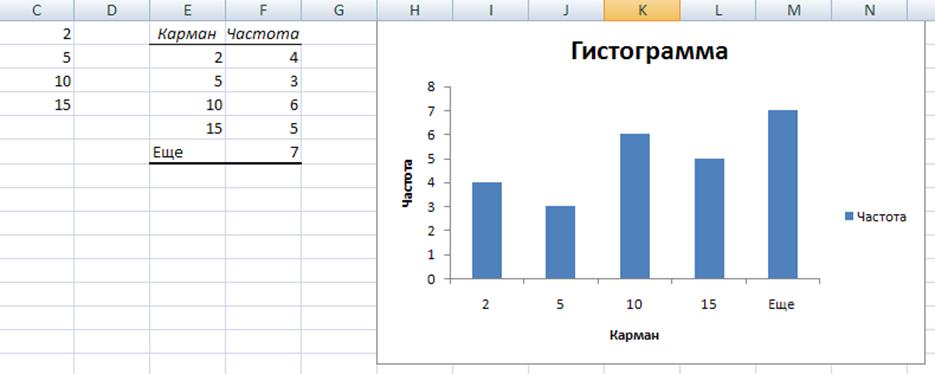
Рис. 10. Результат работы инструмента «Гистограмма».
Для этого воспользуемся формулой: =СУММ((F2-25*1/4))^2/(25*1/4). Запишем ее в ячейку E20. Растянем эту ячейку до E23. Потом рассчитаем сумму.
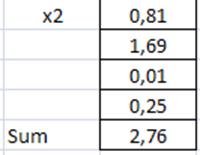
Определяем число степеней свободы v=d-r-1, где d-число интервалов, а r-количество параметров.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.