Изучение имитационного подхода в моделировании на примере системы массового обслуживания – кофейни, страница 5

int TeacherCount=0;

int StudentMax=0;

int ClientCount=0; //Количество посетителей

float Dispersion=0; //Дисперсия

int m=52; //Размер выборки

int ExecutionWaitingTime=0;

int WorkTime=0;

int M=0; //ограничение по колчеству студентов

float N=0; //Количество реализаций

float e=StrToFloat(edAccuracy->Text);

float t=1.7; //Квантиль нормального распределения

TeacherCount=TMod/MatogTeacher; //Максимально допустимое количество пришедших преподавателей

edTeacher->Text=IntToStr(TeacherCount);

StudentMax=TMod/MatogStudent;  //Максимально допустимое количество пришедших студентов

for (int i=0;i<m;i++)

{

Execution=Execution+1;

Dispersion=pow(AverageExecution-Execution,2)/(m-1);

}

N=(Dispersion/sqrt(e))*pow(t,2);

while(N>0)

{

N--;

while(M<StudentMax)

{

M++;

if (Order==0)   //Самый первый посетитель

        {

        Order=Order+1;

        ClientCount=ClientCount+1;

        Execution=Execution+1;

        ExecutionWaitingTime=Application+Execution+Calculation;

        WorkTime=ExecutionWaitingTime;

        }

if (Order>0)   //Если есть очередь

        {

        Order=Order+1;

        ClientCount=ClientCount+1;

        Execution=Execution+1;

        while (WorkTime<=TMod*60)

                {

                ExecutionWaitingTime=ExecutionWaitingTime+TOrder+Application+Execution+Calculation;   //Время выполнения заказа

                WorkTime=ExecutionWaitingTime;  //Время работы буфетчика

                }

        }

if (Order>5)  //Если очередь слишком большая и нет свободных столиков

                        {

                        RefusalCount=RefusalCount+1; //Количество отказавшихся от обслуживания посетителей пишем в счетчик

                        Order=0;

                        }

}

Execution=Execution+1;

}

N=(Dispersion/sqrt(e))*pow(t,2);

if (Kanal>1)

        {

        edRefusal->Text=RefusalCount/Kanal;

        edExecutionWaitingTime->Text=FloatToStr(ExecutionWaitingTime/(ClientCount*Kanal));

        edDownTime->Text=IntToStr(TMod*60-(WorkTime/Kanal));

        edClient->Text=IntToStr(ClientCount+TeacherCount);

        edShare->Text=FloatToStr(ClientCount+TeacherCount-RefusalCount);

        edAverageExecution->Text=FloatToStr(Execution/N);

        }

else

                {

                edRefusal->Text=RefusalCount;                                                            edClient->Text=IntToStr(ClientCount+TeacherCount);

                edExecutionWaitingTime->Text=FloatToStr(ExecutionWaitingTime/ClientCount);

                edDownTime->Text=IntToStr(WorkTime-TMod*60);

                edShare->Text=FloatToStr(ClientCount+TeacherCount-RefusalCount);

                edAverageExecution->Text=FloatToStr(Execution/N);

                }

}

Результаты работы.

1) Изменение параметра «Количество каналов обслуживания».

Доведем количество каналов обслуживания до двух, например, и посмотрим поведение модели.

Среднее время обслуживания снизилось в два раза: с 218 до 115 секунд.

А вот время простоя возросло в 7 раз: с 163 до 875 секунд.

А при количестве каналов обслуживания – 3 среднее время обслуживания снизилось в четыре раза: с 218 до 51 секунд.

А вот время простоя возросло в 10 раз: с 163 до 1152 секунд.

Таким образом, увеличение количества каналов в студенческой кофейне считаем экономически невыгодным, так как возрастает время простоя, а среднее время сокращается таким образом, что нет никакого выигрыша.

Среднее время обслуживания – Количество каналов (в секундах).

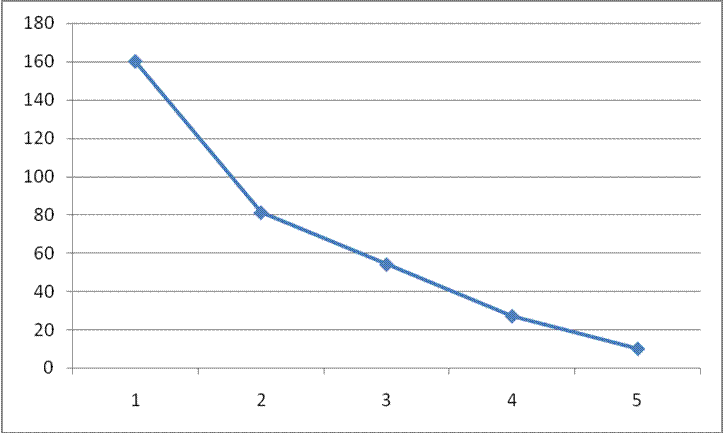
Время простоя кассира – Количество каналов  (в секундах).

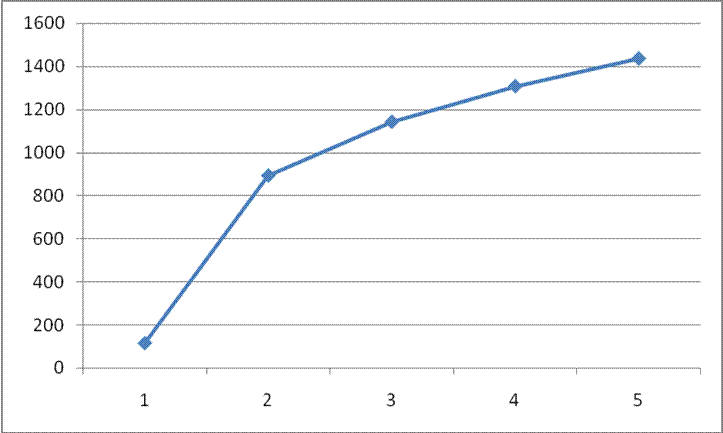
2) Изменение параметра «Время выполнения заказа».