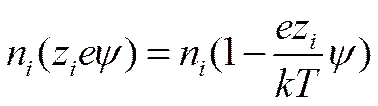Теория межионного взаимодействия. Введение понятий об активности и о коэффициенте активности, страница 5

                  (I I-61)

Были сделаны попытки использовать иные функции распреде­ления. Однако они не получили широкого признания, так как, не повышая существенно степени точности расчетов, осложняли мате­матическое оформление. Использование уравнения (II-61) вместо.

формулы   Больцмана равноценно допущению,  что z_ieψ/kT<1. Это неравенство оправдывается   тем  лучше,   чем ниже концентрация и валентность ионов.

3.  Собственными размерами ионов по сравнению с расстояниями между ними и общим объемом раствора можно пренебречь. Таким образом ионы отожествляются с материальными точками и все их свойства сводятся к величине заряда. Это допущение справедливо только для разбавленных растворов. При повышении концентра­ции ошибка увеличивается и может существенно исказить резуль­таты  расчетов.

4.  Взаимодействие между ионами исчерпывается кулоновскими силами.   Наложение электростатических  сил  на  силы теплового движения  приводит к такому распределению ионов в  растворе, для  которого  характерна  статистическая  шаровая  ионная  атмо­сфера. Это допущение также справедливо лишь для разбавленных растворов.   При   повышении   концентрации   среднее   расстояние между ионами уменьшается и наряду с электростатическими силами появляются другие силы, действующие на более близком расстоя­нии, в первую очередь силы Ван-дер-Ваальса. Понятие об ионной атмосфере в этом случае также должно быть изменено, так как воз­никает необходимость учета не только взаимодействия между дан­ным ионом и его окружением, но и между двумя соседними ионами. Размеры ионной атмосферы при увеличении концентрации и зарядов ионов, как это видно из табл. 7, становятся сравнимыми с соб­ственными размерами ионов, что не согласуется с понятием ионной атмосферы.

ТАБЛИЦА 7

Толщина ионной атмосферы для различных типов электролитов как функция их концентрации (растворитель – вода, t=25°C)                                       

Тип электролита	Толщина ионной атмосферы при концентрации,
	0,001 моль/л	0,01 моль/л	0,1 моль/л
1-1 1-2 и 2-1 2-2 1-3 и 3-1	96,4 55,8 48,2 39,4	30,5 19,3 15,3 13,6	9,64 5,58 4,82 3,94

5. При создании теории молекулярного строения растворов можно использовать диэлектрическую постоянную, которая является макросвойством системы. При расчетах принималось, что диэлектрические постоянные) раствора и чистого растворителя равны. Эти допущения могут быть справедливыми в случае раз­бавленных растворов. Для более концентрированных растворов необходимо учитывать изменение диэлектрической постоянной с концентрацией электролита и иметь в виду, что использование усредненной величины диэлектрической постоянной не будет вполне строгим.

Таким образом, все допущения Дебая и Гюккеля, приводят к тому, что их теория может быть применима только к разбавленным растворам электролитов с ионами низкой валентности. Уравне­ния (II-52 —II-56) и (II-58 —II-60) соответствуют этому предель­ному случаю и выражают так называемый предельный закон Дебая и Гюккеля, или первое приближение теории Дебая и Гюккеля. Поэтому при проверке теории Дебая и Гюккеля в виде предельного закона необходимо учитывать, что сходимость ее с опытом должна ухудшаться по мере увеличения концентрации электролита, повы­шения зарядов его ионов и снижения диэлектрической постоянной раствора.

Предельный закон Дебая — Гюккеля дает правильные значения коэффициентов активности 1-1 валентного электролита (хлористого натрия) особенно в очень разбавленных растворах (табл. 8). По мере увеличения концентрации сходимость теории с опытом ухуд­шается. В случае 2-2 валентного электролита (сульфата цинка) уже при самых малых концентрациях наблюдается расхождение между вычисленными и опытными коэффициентами активности (см. рис. 3 и 4). Так, при концентрации 0,01 моль!л отклонение превы­шает 30%.

ТАБЛИЦА 8

Сопоставление опытных и вычисленных коэффициентов активности растворов и . (Растворитель – вода, t=25°C)