Теория межионного взаимодействия. Введение понятий об активности и о коэффициенте активности, страница 3

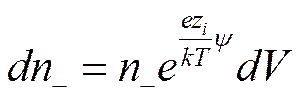
а число положительных

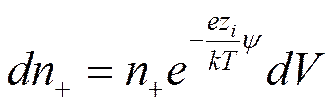
Заряд элемента объема будет равен тогда

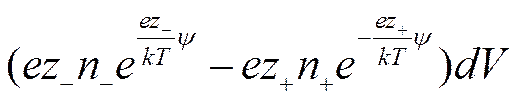
а плотность заряда

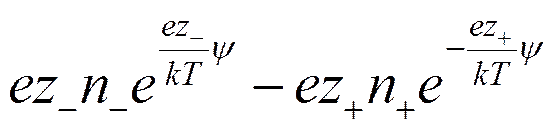
Учитывая, что в растворе находятся различные сорта ионов, и приписывая валентности иона знак, отвечающий его заряду, можно написать, что

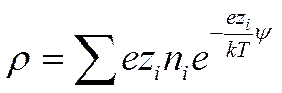                                     (I I -35)

Подставим величину ρ из выражения (II-35)  в  уравнение  Пуас­сона

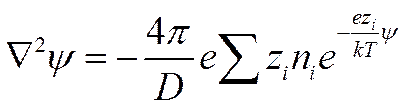                                      (I I-36)

Уравнение (II-36) в его общем виде трудно для решения. Чтобы упростить его, Дебай и Гюккель предположили, что еz_i ψ << kT, т. е. что электростатическое взаимодействие мало по сравнению с термической энергией. Разложив показательную функцию в ряд

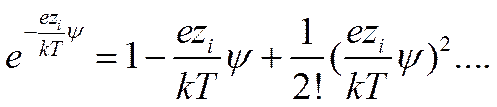                            (I I - 37)

они ограничились  только двумя  его  первыми  членами, получив для ρ следующее уравнение:

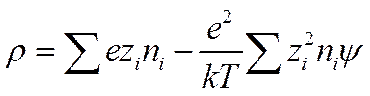                                         (I I-38)

Первый член правой части уравнения (II-38) по закону электро­нейтральности равен нулю, откуда

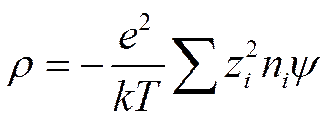
и, следовательно,

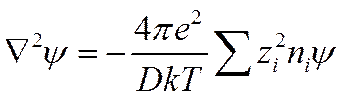                              (I I-39)

или

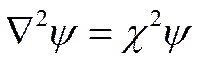                                                   (I I -40)

если ввести обозначение

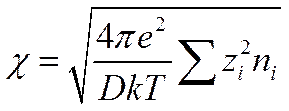                                (I I -41)

Величина χ, точнее 1/ χ, имеет, как это будет показано ниже, большое значение в теории растворов электролитов. Учитывая шаровую симметрию ионной атмосферы, можно вместо V² ψ написать

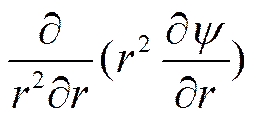                                  (I I-42)

и, подставив это значение V² ψ в уравнение (II-42), получить

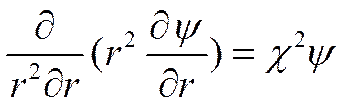                                    (I I-43)

где r— расстояние от центрального иона до места определения потенциала ψ

Общим решением этого дифференциального уравнения будет

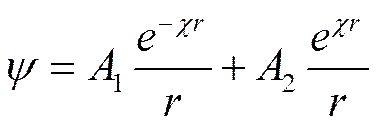                                    (I I-44)

Константы интегрирования A₁ иA₂находят из граничных условий. Как следует из основных законов электростатики, при r->oo ψ -> 0, что является первым граничным условием. Это условие выполняется в том случае, если А₂ = 0, так как иначе с удалением от центрального иона ψ будет стремиться к бесконеч­ности (е ^χr—величина более высокого порядка, чем r). Следова­тельно, при А₂ = О

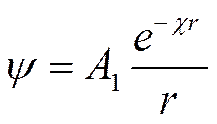                         (I I -45)

Для определения константы интегрирования a₁в первом при­ближении теории Дебая — Гюккеля предполагается, что ионы можно отождествить с материальными точками, обладающими опре­деленным зарядом. В этом случае при г -> 0 потенциал ψ должен стремиться к потенциалу самого иона ψ_iт. е.

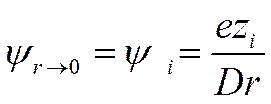                                                            (I I-46)

Если е ^-χr разложить в ряд, то

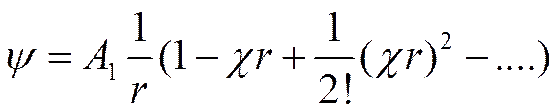
При r -> 0 всеми членами ряда можно пренебречь по сравнению с единицей. Тогда

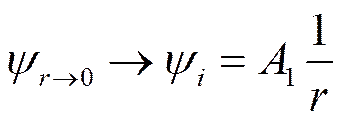
и, следовательно,

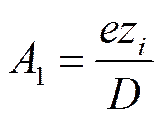                                                         (I I-47)

откуда, а также из (II-45),

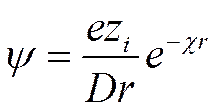                                   (I I-48)

Величина ψ в уравнении (II-48) представляет собой среднее значе­ние потенциала в точке r, создаваемого ионной атмосферой и цен­тральным ионом. Для реальных растворов специфическим является потенциал ионной атмосферы ψ_ia, который находят по правилу суперпозиции потенциалов как разность ψ и ψ_i

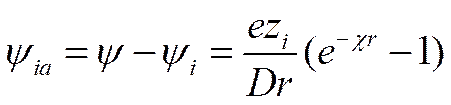
Для вычисления энергии взаимодействия необходимо определить потенциал ионной атмосферы в точке нахождения центрального иона, т. е. найти предел ψ_ia при r->0. Используя вновь тот же прием, т. е. разлагая показательную функцию в ряд и пренебре­гая высшими членами разложения, находим, что

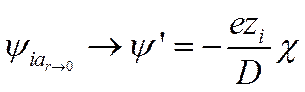                               (I I-49)

Величину ψ’ в соответствии с уравнением (II-49) можно рассматри­вать как потенциал, создаваемый в точке нахождения центрального иона другим ионом с противоположным знаком и находящимся от центрального иона на расстоянии 1/χ. Величина 1/ χ называется характеристической длиной. Так как потенциал создается не еди­ничным ионом, а всей ионной атмосферой, то 1/ χ можно отождест­вить с радиусом ионной атмосферы. Величину χ , а следовательно, и характеристическую длину 1/ χ можно рассчитать по уравнению (II-41).