Как уже отмечалось, в первом приближении теории Дебая — Гюккеля предполагается, что энергия межионного взаимодействия имеет электростатическое происхождение. Энергия взаимодействия между ионами может быть определена поэтому как энергия заряжения центрального иона в электрическом поле ионной атмосферы. Известно, что энергия заряжения частицы от нуля до заряда qв поле ψ равна
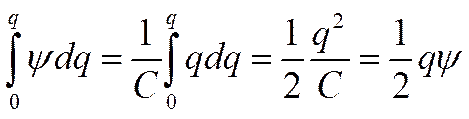(I I-50)
так как q =C ψгде С—емкость.
Подстановка в выражение (II-50) вместо qвеличины заряда центрального иона и вместо ψ -величины ψ’ из уравнения (II-49) приводит к следующему выражению для энергии заряжения, которая равна энергии взаимодействия иона с ионной атмосферой:
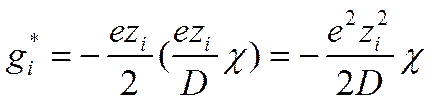(I I-51)
Используя выражение (II-51) в сочетании с (II-30) получим для коэффициента активности
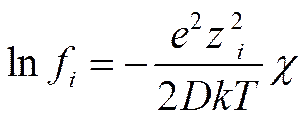(I I-52)
Подставляя значение χ из уравнения (II-41) в (II-52), получим
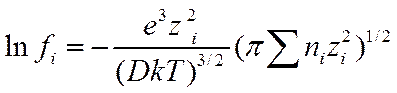(I I-53)
Для перехода от выражения состава раствора через число частиц в единице объема к концентрации в моль!л, величину niнадо заменить на ciNa/1000 . Производя эту замену, получим следующую формулу для коэффициента активности i-го сорта ионов:
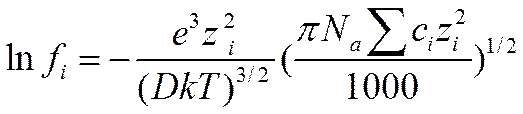(I I-54)
(Здесь и в дальнейшем будем пренебрегать различием между тремя способами выражения коэффициента активности, что вполне допустимо для разбавленных растворов).
В большинстве случаев наряду с коэффициентом активности данного сорта ионов fi нужно знать также и средний коэффициент активности электролита f±, тем более, что опытные данные позволяют найти именно эту величину, а не fi. Выражение для среднего коэффициента активности f± можно получить из (II-54), если учесть, что
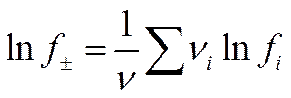
где ν — число ионов, на которое распадается молекула электролита, причем ν = ∑ νi. Это выражение записывают следующим образом:
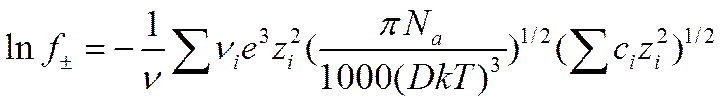(I I-55)
Уравнение (II-55) можно преобразовать, перейдя от натуральных логарифмов к десятичным, введя в него ионную силу J=(1/2)∑ ci zi2 и объединив все независящие от концентрации величины в общую константу h
(I I-56)
где
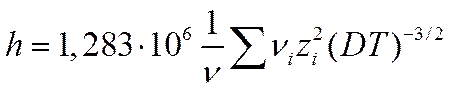(I I-57)
Для бинарного электролита, распадающегося на ионы с валентностями z_ и z+, из уравнений (II-56) и (II-57) следует
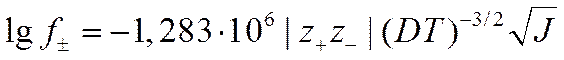(I I-58)
а для бинарного 1-1 валентного электролита
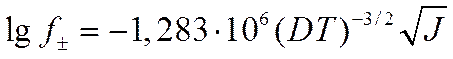(I I-59)
При комнатной температуре (25° С) и диэлектрической постоянной раствора, равной диэлектрической постоянной воды (D = 78,3), для среднего коэффициента активности электролита будет справедлива формула, отвечающая первому приближению теории Дебая и Гюккеля
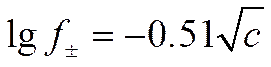(I I-60)
Сопоставление теории Дебая и Гюккеля с опытом. Теория Дебая и Гюккеля позволяет получить такое же уравнение для коэффициента активности, какое было эмпирически найдено для разбавленных растворов электролитов. Теория, следовательно, находится в качественном согласии с опытом. При разработке этой теории были сделаны следующие допущения, которые следует рассмотреть до ее количественного сопоставления с опытом.
1. Число ионов в растворе можно определить из аналитической концентрации электролита, так как он считается полностью диссоциированным (α = 1). Теория Дебая и Гюккеля поэтому иногда называется «теорией полной диссоциации». Однако ее можно применять и в тех случаях, когда α≠1. Действительно, определив из. интенсивности светопоглощения величину степени диссоциации раствора слабого электролита, можно найти истинную концентрацию его ионов, а затем по уравнению (II-60) и средний коэффициент активности.
2. Распределение ионов вокруг любого центрального иона подчиняется классической статистике Максвелла — Больцмана. Физически неясно, насколько классическая статистика может быть приложима к совокупности заряженных частиц, какими являются ионы. Фактически в теории Дебая — Гюккеля используется распределение иного типа, отличное от больцмановского, поскольку после разложения показательной функции в ряд отбрасываются все члены разложения, кроме первого (для несимметричных электролитов) или кроме первых двух (для симметричных электролитов). Эта функция распределения может быть записана как
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.