Основные законы. Уравнения электродинамики Максвелла. Основные соотношения

2. Основные законы. Уравнения электродинамики Максвелла. Основные соотношения. Закон сохранения зарядов. Закон Кулона и закон Гаусса. Закон электромагнитной индукции Фарадея. Законы Ампера, Био-Савара-Лапласса, Максвелла. Уравнения электродинамики Максвелла в вакууме. Электромагнитное поле в вакууме. Уравнения Максвелла для сплошных материальных сред. Процедура Лоренца для получения макроскопических усредненных полей. Четыре формы записи уравнений Максвелла. Системы электромагнитных единиц.

            В этом разделе будут приведены уравнения электродинамики (уравнения Максвелла) для вакуума и для сплошных материальных сред. Эти уравнения являются математическим выражением экспериментальных законов (закон сохранения зарядов, закон Кулона, закон электромагнитной индукции Фарадея, закон Био-Савара-Лапласса, закон Максвелла). Но эти уравнения имеют также эвристический характер, поскольку полностью они не выводились из известных в то время фактов, а получены Максвеллом на основе его убеждения в том, что уравнения для полей  и  должны быть в определенном смысле симметричными. По – сути уравнения Максвелла – это первичные уравнения, постулаты электродинамики.

2.1. Закон сохранения зарядов. Рассмотрим произвольный фиксированный объем , ограниченный поверхностью с единичной внешней нормалью . Этот объем пусть является частью материальной среды с плотностью заряда  (заряд единицы объема) и с плотностью тока (ток, протекающий через единицу поверхности)в ней. Через поверхность  могут втекать и вытекать заряды (Рис.2.1). Будем считать, что внутри объема не происходят реакции, приводящие к появлению или уничтожению заряженных частиц. Ток через поверхность

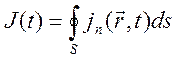
возникает за счет изменения полного заряда в объеме

                                                       .

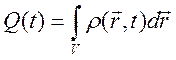       Используем определение тока

                                                       ,

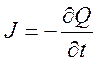где принято, что ток считается положительным, если положительный заряд внутри объема  уменьшается. В результате, с учетом формулы Гаусса-Остроградского (1.3) получим

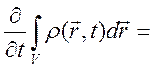
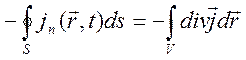                   .                       (2.1)

Будем считать, что внутри объема нет поверхностей, на которых происходит скачкообразное изменение функций  и . Так как объем  в (2.1) произвольный, то из равенства интеграла по объему следует равенство непрерывных подынтегральных  функций:

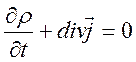                               .                                                      (2.2)

Формулы (2.1) и (2.2) это интегральная и дифференциальная формы закона сохранения зарядов. Эти формы эквивалентны только для непрерывных функций. При необходимости рассматривать разрывные решения, необходимо использовать интегральную форму уравнения в виде закона сохранения. Это относится и к другим законам электродинамики. Запись их в интегральной форме мы будем использовать при получении условий на границе раздела сред (граничных условий). Формулу (2.2) также называют уравнением неразрывности.

            Следует отметить, что закон сохранения (2.2) носит универсальный характер. Функция может быть плотностью того, что сохраняется (плотность энергии, плотность вещества и т.д.), тогда  - это поток того, что сохраняется (поток энергии, поток вещества и т.д.).

            Отметим, что формулы (2.1), (2.2) относятся и к описанию сторонних источников тока и зарядов.

2.2. Закон Кулона и закон Гаусса. Если  - полный сторонний заряд внутри замкнутой поверхности , то закон Кулона (иногда его называют законом Пуассона) для вакуума в интегральной форме имеет вид

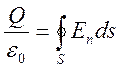                                           ,                                              (2.3)

где обозначения соответствуют Рис.2.1.

В частном случае точечного заряда, в качестве поверхности можно взять сферу радиуса  с центром в месте расположения заряда. Тогда интеграл в (2.3) вычисляется и имеет вид , получается известное представление

                                           .

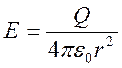В случае, если внутри поверхности находится среда с плотностью заряда, то формула (2.3) с учетом интегрального соотношения Гаусса-Остраградского (1.3) принимает вид

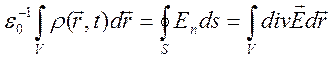                                                 ,              (2.4)

Для функций, непрерывных в объеме , благодаря произвольности этого объема, получаем из (2.4) дифференциальную форму закона Кулона (Пуассона) для вакуума

                                                            ,                                        (2.5)

где - плотность сторонних зарядов.