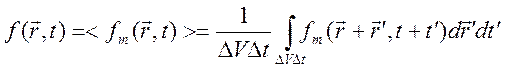Основные законы. Уравнения электродинамики Максвелла. Основные соотношения, страница 5

                                     ,

где линейный размер объема  удовлетворяет двум неравенствам

                                                ,

- средний размер частицы,  - макроскопический масштаб неоднородности усредненных полей, и интервал времени удовлетворяет условию

                                                ,

где , - средняя скорость электронов, - временной масштаб усредненного поля.

Макроскопические поля в результате усреднения системы (2.21)-(2.25) описываются уравнениями Максвелла для сплошной материальной среды (форма №1):

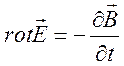,                                                              (2.26)

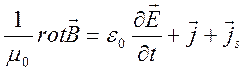,                                          (2.27)

                                                ,                                                        (2.28)

                                                ,                                            (2.29)

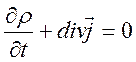                                                ,                                                (2.30)

где ,  , суммирование происходит по всем сортам  заряженных частиц,  - заряд, концентрация, скорость частиц сорта ,  - полная усредненная плотность микроскопического заряда, - полная усредненная плотность микроскопического тока.

            По сравнению с системой (2.21)-(2.25), в полученных уравнениях  (2.26)-(2.30) добавились две новые неизвестные функции . Система уравнений  (2.21)-(2.25) не замкнута. Число уравнений в системе меньше, чем число неизвестных функций. По этой причине, несмотря на линейность этой системы, нельзя сделать вывод об отсутствии нелинейных эффектов. Дополнительные уравнения, описывающие электродинамические свойства конкретной среды могут быть нелинейными. В такой ситуации у волн конечной амплитуды будут проявляться нелинейные эффекты.

            При общем феноменологическом описании сред можно выделить плотность тока свободных зарядов  (плотность тока проводимости),  плотность тока связанных зарядов  за счет смещения их (поляризации) и плотность тока, обусловленную вращением заряженных частиц в атомах и молекулах  :

                                                            .

Молекулярные токи в макроскопическом рассмотрении представляют собой замкнутые вихревые образования , где - вектор намагничивания (магнитный момент единичного объема). Из закона сохранения зарядов следует отсутствие макроскопических молекулярных зарядов, обусловливающих :

.

Плотность зарядов  разбивается только на две части, обусловленные свободными и связанными зарядами

                                                            .

Введя новое вспомогательное поле - вектор напряженности магнитного поля, получим еще один вид записи системы уравнений Максвелла (форма №2):

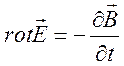,                                      (2.31)

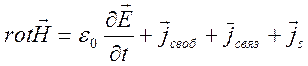,            (2.32)

     ,                                  (2.33)

         ,         (2.34) 

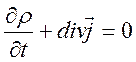       ,                                (2.35)

            Получим третью форму записи уравнений Максвелла для материальных сред, введя два новых векторных поля: вектор поляризации  и вектор электрической индукции . Вектор поляризации  определим как усредненная сумма дипольных моментов связанных и свободных заряженных частиц, содержащихся в единичном объеме

                                                .

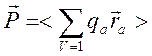Так как для плотности тока имеем представление

                                    ,

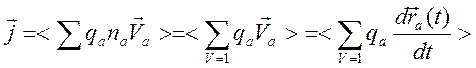то имеем  следующую связь

                                    ,    ,    .

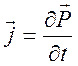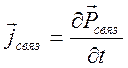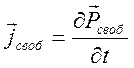В случае движения свободных зарядов наличие  обусловлено движением заряженных частиц. Используя закон сохранения зарядов

                                                ,

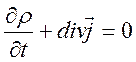можно получить связь между плотностью зарядов и вектором поляризации