Основные законы. Уравнения электродинамики Максвелла. Основные соотношения, страница 2

Максвелл первым допустил, что формулы  (2.3), (2.5) справедливы не только для задач статики, но и для электродинамики в вакууме (о законе Кулона для сплошных материальных сред будем говорить позже). В частном случае будем иметь , что означает непрерывность электрических силовых линий при отсутствии заряженных частиц

            В природе нет магнитных зарядов, поэтому аналогами формул (2.3) - (2.5) для магнитной индукции  будет закон Гаусса

                                               

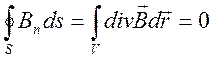
                                                            .                                            (2.6)

            Из (2.6) следует, что силовые линии поля имеют непрерывную вихревую структуру и возможно представление . Функция  называется векторным потенциалом, она определяется неоднозначно. Так как , где  - произвольная функция, то векторные потенциалы  и  будут приводить к одной и той же магнитной индукции.

2.3. Закон электромагнитной индукции Фарадея. Пусть замкнутый проводник  имеет длину больше, чем диаметр поперечного сечения этого проводника и он «охватывает» площадь  (см. рис.2.1). Циркуляция  (эта циркуляция обычно называется электродвижущей силой -ЭДС) вектора  вдоль контура  имеет представление согласно определению

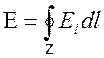                                                .                                          (2.7)

Из экспериментов известно, что ЭДС  определяется изменением во времени потока   магнитной индукции через площадь

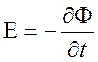                                           ,                                           (2.8)

где поток  имеет представление

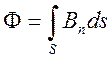                                                .                                        (2.9)

На основе (2.7)-(2.9) с учетом формулы Стокса (1.4) и произвольности площади получается закон индукции Фарадея для замкнутого проводника в вакууме

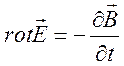                                                .                                      (2.10)

Максвелл обобщил законы (2.7)-(2.10) на воображаемый (не реальный) контур в вакууме (на самом деле закон (2.10) справедлив и для сплошной материальной среды).

2.4. Законы Ампера, Био-Савара-Лапласса, Максвелла. В электростатике существует закон Кулона, описывающий взаимодействие двух зарядов

                                                .

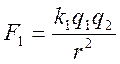Ампером был открыт закон взаимодействия двух токов: между двумя длинными параллельными проводами , по которым протекают токи  и  возникает сила взаимодействия  пропорциональная произведению сил этих токов, пропорциональная длине  проводов и обратно пропорциональная расстоянию между проводами. Параллельные токи притягиваются, а антипараллельные – отталкиваются.

                                                ,

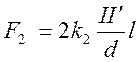где множитель 2 введен для удобства, - константа аналогичная константе  в законе Кулона. Напомним связь между током и зарядом

                                                .

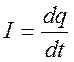Из сравнения размерностей функций в законах Кулона и Ампера следует, что  имеет размерность квадрата скорости. Экспериментальное сравнение сил  и  показывает, что в любой системе единиц имеется место соотношение

                                                            ,

где  - скорость света в вакууме. В гауссовой системе . В системе СИ, как отмечалось выше . Введем вторую константу , аналогичную соотношением

                                                           

и получим представление для константы  ( - единица индуктивности генри).

Введем теперь понятие магнитной индукции. Пусть замкнутый контур  охватывает площадку   как показано на Рис.2.1. Экспериментально установлен закон полного тока для задач статики:

                                                ,                                     (2.11)