Основные законы. Уравнения электродинамики Максвелла. Основные соотношения, страница 3

где  - циркуляция  вектора магнитной индукции вдоль замкнутого контура

                                                ,

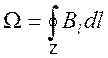а полный ток - это ток, пронизывающий контур

                                                .

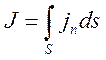Направление векторов  и  связано правилом буравчика (Рис.2.2). В формуле (2.11) - размерная величина с размерностью в системе СИ  (размерность полей и параметров в электродинамике будет обсуждаться ниже) и справедливо представление .

            Воспользуемся формулой Стокса 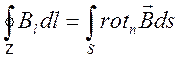 и получим закон Био-Савара-Лапласса (для статики) в интегральной форме

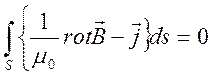                                     (2.12)

и для непрерывных функций, пользуясь произвольностью площади можно из (2.12) получить закон Био-Савара-Лапласса (для статики) в дифференциальной форме

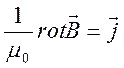.                                                              (2.13)

В вакууме нет носителей заряда, плотность тока  в формулах (2.12), (2.13) это плотность стороннего тока, протекающего в реальном замкнутом контуре.  Для определения магнитостатических полей в вакууме у нас есть два уравнения, одно для дивергенции (закон Кулона), а другое для ротора вектора магнитной индукции (2.13).

Максвеллом сделано обобщение (2.13) на случай переменных во времени полей (для задач электродинамики). Он добавил из соображений симметрии с законом индукции Фарадея одно слагаемое – плотность тока смещения в вакууме 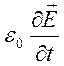. Полученное таким образом уравнение характеризует закон Максвелла:

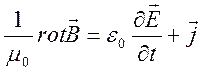                                    .                                                 (2.14)

Это уравнение, в частности утверждает, что при отсутствии стороннего тока () магнитная индукция  может возникать за счет изменения электрического поля во времени (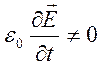). В задачах динамики электрическое и магнитное поля взаимосвязаны – существуют электромагнитные волны. На основании своих уравнений, сформулированных в 1860-1865 гг., Максвелл в 1865 г. предсказал существование электромагнитных волн, распространяющихся со скоростью света 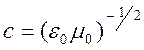 в вакууме. Он предположил, что видимый свет – это электромагнитная волна определенной длины (частоты).

2.5. Уравнения электродинамики Максвелла в вакууме. Электромагнитное поле в вакууме. На основе анализа нестационарных полей в вакууме, мы пришли к системе пяти уравнений

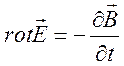,                                      (2.15)

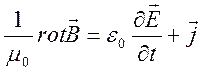,                         (2.16)

,                                            (2.17)

,                                        (2.18)

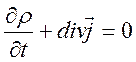.                                    (2.19)

Следует отметить, что уравнения (2.17), (2.18) являются следствиями (2.15) и (2.16), при учете нулевых начальных условий и закона сохранения зарядов в стороннем источнике (2.19). Покажем это. Так как , где  произвольный вектор, то из уравнений (2.15) и (2.16) получаем

                                    ,     

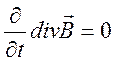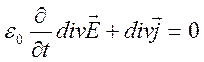
и при учете закона сохранения зарядов (2.19) имеют место соотношения

                                    ,       ,

где - не зависящие от времени произвольные функции координат. Рассматривая задачу о возбуждении полей сторонними токами и зарядами, необходимо считать, что при  выполняются  начальные условия  поэтому. В результате приходим к уравнениям (2.17), (2.18) .

            При заданном стороннем токе , система уравнений (2.15), (2.16) является замкнутой: число уравнений равно числу неизвестных функций. Эта система уравнений линейна, значит, нелинейные эффекты этой системой не описываются, для полей  справедлив принцип линейной суперпозиции. Уравнения  (2.15), (2.16) справедливы в системе единиц СИ в произвольной системе координат.