Основные законы. Уравнения электродинамики Максвелла. Основные соотношения, страница 4

            Переменные во времени поля  и  влияют друг на друга. Возникает вопрос: не могут ли они «поддерживая друг друга», существовать в вакууме без сторонних зарядов и токов? Математически вопрос сводится к тому, имеют ли однородные () уравнения Максвелла нетривиальные решения. Не трудно убедиться, что таких решений бесконечно много. Исключим из системы индукцию , приняв во внимание представление

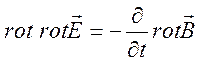
и уравнение (2.16), получим уравнение для электрического поля

                                    .

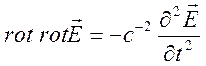Учтем, что   и при отсутствии сторонних зарядов . В результате получим волновое уравнение

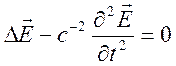                                    .                                                      (2.20)

Можно убедиться, что такому же уравнению удовлетворяет индукция . Ограничимся рассмотрением полей , уравнение (2.20) имеет решение                                                                                  ,

где - произвольные функции. При этом функция  описывает стационарную волну, (ее профиль сохраняется в процессе распространения) распространяющуюся со скоростью света  в вакууме  в сторону . Аналогично  описывает волну, распространяющуюся в противоположном направлении. Эти волны называются электромагнитными волнами, они имеют поперечную структуру: векторы  и  перпендикулярны направлению распространения – вектору . Кроме этого векторы  и  ортогональны друг другу.

            Приходим к выводу, что переменные во времени электромагнитные поля могут существовать в вакууме при отсутствии сторонних зарядов и токов. Это значит, что электромагнитное поле – это физическая реальность, а не чисто формальное понятие, атрибут зарядов и токов. Можно показать, что электромагнитное поле, как и вещество, обладает энергией, импульсом и моментом.

            Уравнения Максвелла представляют собой законы движения электромагнитного поля, так же как законы Ньютона являются законами механического движения вещества.

2.6. Уравнения Максвелла для сплошных материальных сред. Процедура Лоренца для получения макроскопических усредненных полей. Четыре формы записи уравнений Максвелла. Установим уравнения, описывающие электродинамические процессы в веществе. При классическом (не квантовом) описании, вещество – вакуум, в котором могут быть нейтральные и заряженные частицы. Заряженные частицы испытывают влияние электромагнитного поля и сами модифицируют это поле. Возникает задача о самосогласованном взаимодействии электромагнитного поля в вакууме и электронов, ионов и ядер атомов вещества. Задача эта впервые бала сформулирована Лоренцем в конце 19 века, и он же в 1902 г. предложил решение ее. Истинные (микроскопические поля) в вакууме, модифицированные заряженными частицами вещества характеризуются чрезвычайной нерегулярностью. Движущиеся заряженные частицы вещества и наводимые ими токи являются дополнительными, сторонними источниками полей в вакууме. Поэтому для микроскопических полей (ниже они отмечены индексом ) будем иметь систему аналогичную (2.15)-(2.19) (иногда эту систему называют уравнениями Максвелла-Лоренца):

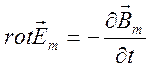,                                              (2.21)

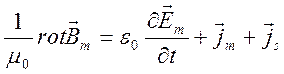,                        (2.22)

,                                                      (2.23)

,                                        (2.24)

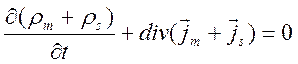.                     (2.25)

Эта система уравнений описывает поля в вакууме, в котором «плавают» заряженные частицы вещества. Большая нерегулярность микроскопических полей обусловлена малыми (атомарными) размерами частиц. Эта нерегулярность полей для многих задач несущественна, так как интерес представляют усредненные поля не содержащие эти мелкие нерегулярности. При этом нужно ввести понятие усредненных макроскопических полей. Сделано это было Лоренцом (1902 г.) на основе процедуры усреднения в окрестности точки наблюдения  и времени наблюдения  по физически бесконечно малому объему и интервалу времени  по формуле