Математика \ Математический анализ

Криволинейные и поверхностные интегралы в пространстве

Страницы работы

15 страниц (Word-файл)

Скачать файл

Содержание работы

Криволинейные и поверхностные интегралы в пространстве

Ответ:1

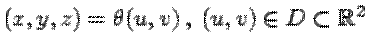Простая гладкая поверхность $\Gamma$ в $\mathbb{R}^{3}$ задается параметрически отображением $(x,y,z)=\theta (u,v)\,,\;(u,v)\in D\subset \mathbb{R}^{2}$ , ранг производной (матрицы Якоби) которого равен 2. Переменные называются локальными координатами на $\Gamma$ . Ориентация поверхности $\Gamma$ определяется как ориентация области изменения локальных координат (т.е. ориентацией пространства $\mathbb{R}^{2}$ ). Например, изменение порядка локальных координат меняет ориентацию поверхности $\Gamma$ на противоположную. Выбор ориентации поверхности можно осуществить выбором базиса касательных векторов, например,

$\displaystyle \tau_{1}= \frac{\partial\theta}{\partial u}\,,\qquad \tau_{2}=\frac{\partial\theta}{\partial v}\,,$

непрерывно зависящих от точки поверхности. Такое определение ориентации можно распространить и на поверхности, не являющиеся простыми. Наконец, ориентацию поверхности можно задать выбором вектора единичной нормали $\mathbf{n}$ , непрерывно зависящего от точки поверхности. При этом надо пользоваться соглашением: вектор $\mathbf{n}$ определяет ту же ориентацию, что и касательные вектора $\tau_{1},\tau_{2}$ , если базис векторов $\mathbf{n},\tau_{1},\tau_{2}$ задает ориентацию пространства $\mathbb{R}^{3}$ . О выборе вектора нормали говорят как о выборе стороны поверхности $\Gamma$ .

Ориентация связной области пространства $\mathbf{R}^{3}$ определяется как ориентация самого пространства $\mathbb{R}^{3}$ , т.е. выбором класса эквивалентных между собой базисов. При этом, два базиса векторов в $\mathbb{R}^{3}$ считаются эквивалентными, если переход от одного из них к другому осуществляется матрицей перехода, имеющей положительный определитель. Ориентацию пространства можно задать также выбором формы объема $\Omega$ -- невырожденной 3-формы. Форма $\Omega$ определяет ту же ориентацию, что и базис $\mathbf{e}_{1},\mathbf{e_{2}}, \mathbf{e_{3}}$ , если $\Omega (\mathbf{e}_{1},\mathbf{e_{2}}, \mathbf{e_{3}})>0$ .

Ответ: 2

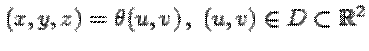Всякая простая поверхность допускает ориентацию. Простая гладкая поверхность $\Gamma$ в $\mathbb{R}^{3}$ задается параметрически отображением $(x,y,z)=\theta (u,v)\,,\;(u,v)\in D\subset \mathbb{R}^{2}$ , ранг производной (матрицы Якоби) которго равен 2. Переменные называются локальными координатами на $\Gamma$ . Ориентация поверхности $\Gamma$ определяется как ориентация области изменения локальных координат (т.е. ориентацией пространства $\mathbb{R}^{2}$ ). Например, изменение порядка локальных координат меняет ориентацию поверхности $\Gamma$ на противоположную. Выбор ориентации поверхности можно осуществить выбором базиса касательных векторов, например,

$\displaystyle \tau_{1}= \frac{\partial\theta}{\partial u}\,,\qquad \tau_{2}=\frac{\partial\theta}{\partial v}\,,$

Поверхность, не являющаяся простой может не быть ориентируемой. Это означает, что на этой поверхности не существует непрерывно зависящего от точки поверхности базисного репера $\tau_{1},\tau_{2}$ касательных векторов, определяющих ориентацию касательных плоскостей. Это же означает, что непрерывно перемещая вектор единичной нормали к поверхности по замкнутому пути можно так выбрать этот путь, что при возвращении в исходную точку направление вектора нормали изменится на противоположное. Такие поверхности называются односторонними. Односторонние поверхности не ориентируемы. Примером односторонней поверхности в $\mathbb{R}^{3}$ является лист Мебиуса.

$\includegraphics{mebius.mps}$

Рис.: Лист Мебиуса

В $\mathbb{R}^{3}$ все двусторонние поверхности являются ориентируемыми

Ответ:3а

Гладкая кривая $\Gamma$ в пространстве $\mathbb{R}^{3}$ задается параметрически как образ некоторого гладкого пути $\gamma (t),\;t\in[a,b]$ , в координатном виде:

$\displaystyle x=x (t) ,\quad y=y(t) ,\quad z=z (t) .$

Если $\gamma (a)=\gamma (b)$ , край кривой пуст. В противном случае краем $\partial\Gamma$ кривой называется множество $\{A,B\}$ ее концов: $\{A,B\}=\{\gamma (a), \gamma (b)\}$ .

Ориентацию кривой можно определить выбором одного из двух единичных касательных векторов

$\displaystyle \pm\frac{\gamma' (t)}{\vert\gamma' (t)\vert} ,$

непрерывно зависящих от точки $\gamma (t)$ кривой. Под ориентацией края кривой понимают упорядочение множества $\partial\Gamma$ .

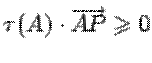Если касательный вектор $\tau$ задает ориентацию кривой $\Gamma$ , то согласованную ориентацию ее края $\partial\Gamma$ определяют как пару концов такую, что $\tau (A)$ является внутренним по отношению к краю вектором, т.е. $\tau (A)\cdot \overrightarrow{AP}\geqslant0$ для точек кривой, достаточно близких к точке .

Ответ:3б

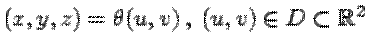Простая гладкая поверхность $\Gamma$ в $\mathbb{R}^{3}$ задается параметрически отображением $(x,y,z)=\theta (u,v)\,,\;(u,v)\in D\subset \mathbb{R}^{2}$ , ранг производной (матрицы Якоби) которого равен 2. Ее краем $\partial\Gamma$ называется образ границы области : $\partial\Gamma=\theta (\partial D)$ . Край поверхности это кусочно гладкая замкнутая кривая.