Математика \ Математический анализ

Криволинейные и поверхностные интегралы в пространстве, страница 4

$\displaystyle \imath_{\mathbf{v}} (\alpha\wedge\beta)= (\imath_{\mathbf{v}}\alpha)\wedge\beta + (-1)^{k}\alpha\wedge (\imath_{\mathbf{v}}\beta) ,$

где $ k$-- порядок формы $ \alpha$.

Ответ:8

 Будем считать, что гладкая поверхность $ G$в $ \mathbb{R}^{3}$задается параметрически вектор-функцией $ \theta: \;D\to \mathbb{R}^{3}$, определенной на плоском множестве $ D$, причем $ \mathrm{rank\,}\theta'=2$(столбцы в матрице Якоби линейно независимы). Координаты на $ D$обозначим через $ u$и $ v$, они называются локальными координатами на поверхности $ G$. Функцию $ \theta$называют параметризацией поверхности $ G$. Вводя стандартные координаты $ (x,y,z)$в $ \mathbb{R}^{3}$, определим функцию $ \theta$равенствами

$\displaystyle x=x (u,v)\,,\qquad y=y (u,v)\,,\qquad z=z (u,v)\,.$

Под ориентацией поверхности $ G$будем понимать ориентацию области изменения локальных координат -- ориентацию области $ D$. Последняя определяется порядком локальных координат, пусть это будет именно $ (u,v)$. Рассмотрим 2-форму $ \omega$

$\displaystyle \omega=A (x,y,z)\,dy\wedge dz+B (x,y,z)\,dz\wedge dx+C (x,y,z)\,dx\wedge dy\,,$


считая, что коэффициенты $ A,B,C$заданы в точках поверхности $ G$. Сужением формы $ \omega$на параметризованную поверхность $ G$называется 2-форма

$\displaystyle \theta^{*}\omega=f (u,v)\,du\wedge dv\,,$

где

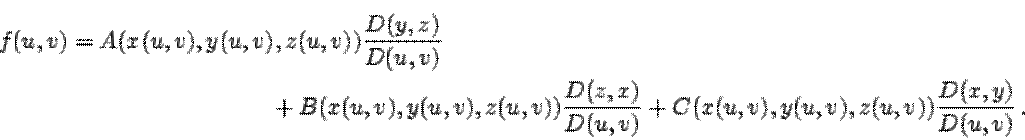
\begin{multline*} f (u,v)= A (x (u,v),y (u,v),z (u,v)) \frac{D (y,z)}{D (u,v)}\\... ...D (u,v)}+ C (x (u,v),y (u,v),z (u,v)) \frac{D (x,y)}{D (u,v)}\,. \end{multline*}


По определению

$\displaystyle \int\limits_{G}\omega=\int\limits_{D}\theta^{*}\omega=\int\limits_{D}f (u,v)\,dudv\,.$

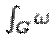Как видно, определение зависит от ориентации поверхности. Если изменить ориентацию, то в силу $ dv\wedge du=-du\wedge dv$интеграл $ \int_{G}\omega$изменит знак. Вместе с тем, при сохранении ориентации определение не зависит от выбора параметризации поверхности. Последнее вытекает из формулы замены переменных в двойном интеграле.

Ответ:9

 Будем считать, что гладкая поверхность $ G$в $ \mathbb{R}^{3}$задается параметрически вектор-функцией $ \theta: \;D\to \mathbb{R}^{3}$, определенной на плоском множестве $ D$, причем $ \mathrm{rank\,}\theta'=2$(столбцы в матрице Якоби линейно независимы). Координаты на $ D$обозначим через $ u$и $ v$, они называются локальными координатами на поверхности $ G$. Функцию $ \theta$называют параметризацией поверхности $ G$. Вводя стандартные координаты $ (x,y,z)$в $ \mathbb{R}^{3}$, определим функцию $ \theta$равенствами

$\displaystyle x=x (u,v)\,,\qquad y=y (u,v)\,,\qquad z=z (u,v)\,.$


Под ориентацией поверхности $ G$будем понимать ориентацию области изменения локальных координат -- ориентацию области $ D$. Последняя определяется порядком локальных координат, пусть это будет именно $ (u,v)$. Рассмотрим 2-форму $ \omega$

$\displaystyle \omega=A (x,y,z)\,dy\wedge dz+B (x,y,z)\,dz\wedge dx+C (x,y,z)\,dx\wedge dy\,,$

считая, что коэффициенты $ A,B,C$заданы в точках поверхности $ G$. Сужением формы $ \omega$на параметризованную поверхность $ G$называется 2-форма

$\displaystyle \theta^{*}\omega=f (u,v)\,du\wedge dv\,,$

где

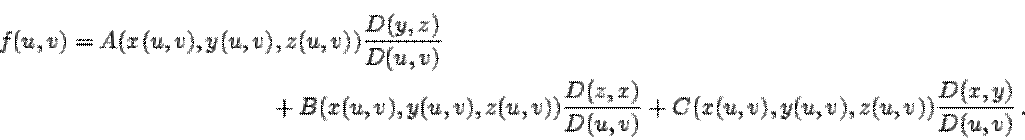
\begin{multline*} f (u,v)= A (x (u,v),y (u,v),z (u,v)) \frac{D (y,z)}{D (u,v)}\\... ...D (u,v)}+ C (x (u,v),y (u,v),z (u,v)) \frac{D (x,y)}{D (u,v)}\,. \end{multline*}


По определению

$\displaystyle \int\limits_{G}\omega=\int\limits_{D}\theta^{*}\omega=\int\limits_{D}f (u,v)\,dudv\,.$

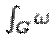Как видно, определение зависит от ориентации поверхности. Если изменить ориентацию, то в силу $ dv\wedge du=-du\wedge dv$интеграл $ \int_{G}\omega$изменит знак. Вместе с тем, при сохранении ориентации определение не зависит от выбора параметризации поверхности. Последнее вытекает из формулы замены переменных в двойном интеграле.

Ответ:10

Поверхностный интеграл 2 рода это интеграл от дифференциальной 2-формы по ориентированной поверхности в $ \mathbb{R}^{3}$:

$\displaystyle I=\iint\limits_{\Gamma}A (x,y,z) dy\wedge dz+ B (x,y,z) dz\wedg... ...+ C (x,y,z) dx\wedge dy= \iint\limits_{\Gamma} \mathbf{F}\cdot d \mathbf{S} ,$


где $ \mathbf{F}= (A,B,C)$и $ d \mathbf{S}= (dy\wedge dz, dz\wedge dx, dx\wedge dy)$. Если поверхность $ \Gamma$имеет параметризацию

$\displaystyle x=x (u,v) ,\qquad y=y (u,v) ,\qquad z=z (u,v) ,\qquad (u,v)\in D ,$


то значение поверхностного интеграла находится по формуле

$\displaystyle I= \iint\limits_{D} \left[ A \frac{D (y,z)}{D (u,v)} +B \frac{D (z,x)}{D (u,v)}+C \frac{D (x,y)}{D (u,v)}\right] dudv ,$

где $ A,B$и $ C$должны рассматриваться уже как сложные функции переменных $ u,v$.

Вектор

$\displaystyle \boldsymbol{N}= \Bigl( \frac{D (y,z)}{D (u,v)} , \frac{D (z,x)}{D (u,v)} , \frac{D (x,y)}{D (u,v)} \Bigr)$


является нормальным (вообще говоря, не единичным) к поверхности. Его орт обозначим через $ \boldsymbol{n}$. Тогда

$\displaystyle \iint\limits_{\Gamma} \mathbf{F}\cdot d \mathbf{S}= \iint\limits_{\Gamma} \mathbf{F}\cdot \boldsymbol{n}\,dS\,.$

Эта формула и выражает упомянутую связь.

Ответ: 11

Пусть $ D$-- связная жорданова область в $ \mathbb{R}^{3}$с координатами $ (x,y,z)$. Данный порядок координат определяет ориентацию пространства и области $ D$. Пусть далее $ \omega$-- дифференциальная 3-форма, определенная на области $ D$. Тогда она может быть записана в виде $ \omega=f (x,y,z) dx\wedge dy\wedge dz$. По определению, интеграл от формы $ \omega$по ориентированной области $ D$равен тройному интегралу от функции $ f$по данной области:

$\displaystyle \iiint\limits_{D}\omega= \iiint\limits_{D}f (x,y,z) dxdydz .$


Эта формула, в частности, выражает связь между интегралом от 3-формы и тройным интегралом.

При изменении ориентации пространства (области) функция $ f$-- множитель перед базисной 3-формой, определяющей ориентацию, -- изменит знак. Это означает, что в отличии от тройного интеграла интеграл от 3-формы зависит от ориентации области интегрирования.

Скачать файл