Математика \ Математический анализ

Криволинейные и поверхностные интегралы в пространстве, страница 6

В классических обозначениях $ \omega= \mathbf{F}\cdot \boldsymbol{dS}$и $ d\omega= \mathrm{div\,} \mathbf{F}\, dx\wedge dy\wedge dz$, где $ \mathbf{F}= (A,B,C)$, $ \boldsymbol{dS}= (dy\wedge dz, dz\wedge dx, dx\wedge dy)$. Учитывая связь интегралов 1 и 2 родов, формула Стокса может быть переписана в виде

$\displaystyle \iiint\limits_{\Gamma} \mathrm{div\,} \mathbf{F} \,dV= \iint\limits_{\partial\Gamma} \mathbf{F}\cdot \mathbf{n} \,dS\,.$

Полученная формула читается (справа налево) как: поток вектора через поверхность тела $ \Gamma$равен интегралу от дивергенции вектора. Эта формула и называется формулой Гаусса-Остроградского

Ответ: 18а

1-форма на плоскости, являющаяся дифференциалом функции называется точной. Интеграл от точной формы не зависит от пути интегрирования. Верно и обратное. Если интеграл от 1-формы не зависит от пути интегрирования, форма является точной. Потенциал $ f$такой формы $ \omega$может быть найден по формуле

$\displaystyle f (x,y)= \int\limits_{(x_{0},y_{0})}^{(x,y)}\omega ,$


где $ (x_{0},y_{0})$-- произвольная фиксированная точка из области определения формы $ \omega$, а путь, соединяющий начало и конец выбран произвольно.

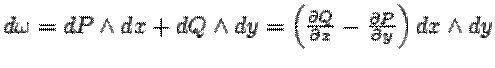Необходимым условием точности формы является ее замкнутость: $ d\omega=0$. В координатах, $ \omega=P dx+Q dy$и $ d\omega= dP\wedge dx+ dQ\wedge dy= \left( \frac{\partial Q}{\partial x}- \frac{\partial P}{\partial y} \right)dx\wedge dy$и условие замкнутости примет вид

$\displaystyle \frac{\partial P}{\partial y}= \frac{\partial Q}{\partial x} .$

Это условие будет достаточным для точности формы, если область определения формы односвязна (стягивается в точку). В окрестности нуля потенциал может быть восстановлен по формуле Пуанкаре

$\displaystyle f (x,y)= \int\limits_{0}^{1}dt [P (tx,ty) x+Q (tx,ty) y] ,$


что соответствует интегрированию формы $ \omega$по отрезку прямой, соединяющему начало координат и точку $ (x,y)$.

Ответ:18б

Форма $ \omega$называется точной, если она имеет вид внешнего дифференциала некоторой формы $ \alpha$, называемой потенциалом (первообразной) формы $ \omega$: $ \; \omega=d\alpha\,. $

Форма $ \omega$называется замкнутой, если ее внешний дифференциал равен нулю: $ \; d\omega=0$.

В силу леммы Пуанкаре точные формы являются замкнутыми: $ \; dd\alpha=0$.

Обратное верно, вообще говоря, только локально: замкнутая форма локально является точной (теорема Пуанкаре). Например, в окрестности нуля он может быть восстановлен по формуле

$\displaystyle \alpha= \int\limits_{0}^{1}dt\, \theta_{t}^{*}\imath_{\mathbf{v}} \omega\,,$

где $ \theta_{t} ( \mathbf{x})=t \mathbf{x}$и $ \mathbf{v}= \frac{\mathbf{x}}{t}\,, \;t\in [0,1]$.

Потенциал точной формы определен неоднозначно. Если $ \alpha$-- потенциал формы $ \omega$, то $ \beta=\alpha+ d\gamma$-- тоже потенциал (в силу леммы Пуанкаре).

Ответ:19

Форма $ \omega$называется точной, если она имеет вид внешнего дифференциала некоторой формы $ \alpha$, называемой потенциалом (первообразной) формы $ \omega$: $ \; \omega=d\alpha\,. $

В силу леммы Пуанкаре, $ dd=0$. Это означает, что для того, чтобы форма была точна, необходимо, чтобы она была замкнута, т.е. чтобы внешний дифференциал ее был равен нулю: $ \; d\omega=0$.

Однако не любая замкнутая форма является точной. Для того, чтобы замкнутая форма была точной в некоторой области достаточно, чтобы эта область могла быть стянута в точку.

В случае 1-форм в пространстве условия на область можно ослабить. Например, для точности замкнутой 1-формы в пространстве достаточно, чтобы любой замкнутый (гладкий) контур можно было стянуть в точку.

Ответ: 20

1-форма $ \omega$называется точной, если она имеет вид внешнего дифференциала некоторой функции $ f$, называемой потенциалом (первообразной) формы $ \omega$: $ \; \omega=df\,. $Потенциал определен с точностью до константы.

Если 1-форма $ \omega$точна, то по формуле Стокса

$\displaystyle \int\limits_{\Gamma}\omega= \int\limits_{\Gamma}df= \int\limits_{\partial\Gamma}f=f (B)-f (A)\,,$


где $ A$и $ B$-- начало и конец кривой $ \Gamma$. Эта формула позволяет восстановить потенциал в виде

$\displaystyle f ( \mathbf{x})= \int\limits_{ \mathbf{x}_{0}}^{ \mathbf{x}}\omega\,,$

где $ \mathbf{x}_{0}$-- произвольная фиксированная точка, $ \mathbf{x}$-- переменная точка, а контур, соединяющий $ \mathbf{x}_{0}$с $ \mathbf{x}$выбран произвольно.

Если этот контур можно выбрать в виде отрезка прямой, идущей из нуля, получим формулу Пуанкаре:

$\displaystyle f (\mathbf{x})= \int\limits_{0}^{1}dt\,[ P ( t \mathbf{x})x+ Q (t \mathbf{x})y+ R (t \mathbf{x})z]\,,$

где $ \mathbf{x}= (x,y,z)$и $ \omega=P ( \mathbf{x})\,dx+ Q ( \mathbf{x})\,dy+ R ( \mathbf{x})\,dz$.

Ответ: 21

2-форма $ \omega$называется точной, если она имеет вид внешнего дифференциала некоторой 1-формы $ \alpha$, называемой потенциалом (первообразной) формы $ \omega$: $ \; \omega=d\alpha\,. $Потенциал определен с точностью до дифференциала функции.

Потенциал точной формы в окрестности любой точки из области определения может быть восстановлен по формуле Пуанкаре. В окрестности нуля она имеет вид

$\displaystyle \alpha (\mathbf{x})= \int\limits_{0}^{1}dt\,t[ P ( t \mathbf{x})(y\,dz-z\,dy)+ Q (t \mathbf{x})(z\,dx-x\,dz)+ R (t \mathbf{x}) (x\,dy-y\,dx)]$

$\displaystyle = \int\limits_{0}^{1}dt \begin{vmatrix}dx& dy&dz\\ P (t \mathbf{x})& Q (t \mathbf{x})& R (t \mathbf{x})\\ tx&ty&tz \end{vmatrix}\,.$


где $ \mathbf{x}= (x,y,z)$и $ \omega=P ( \mathbf{x})\,dy\wedge dz+ Q ( \mathbf{x})\,dz\wedge dx+ R ( \mathbf{x})\,dx\wedge dy$.

Скачать файл