Математика \ Математический анализ

Ответы на контрольные задания по теме: "Кратные интегралы"

Страницы работы

8 страниц (Word-файл)

Посмотреть все страницы

Скачать файл

Фрагмент текста работы

Кратные интегралы

Ответ: 1

Определим сначала двойной интеграл от функции по прямоугольнику . Пусть $\lambda$ -- разбиение прямоугольника, получающееся дроблением его сторон. Для ячейки разбиения $\lambda$ положим

$\displaystyle m_{A}=\inf_{A}f ,\qquad M_{A}=\sup_{A}f$

и введем нижнюю и верхнюю суммы Дарбу

$\displaystyle \sigma_{*} (f,\lambda)=\sum m_{A}S (A) ,\qquad \sigma^{*} (f,\lambda)=\sum M_{A}S (A) ,$

где -- площадь ячейки . При продолжении разбиения нижняя сумма Дарбу $\sigma_{*}$ может лишь увеличиться, а верхняя -- лишь уменьшиться. Если

$\displaystyle \sup \sigma_{*} (f,\lambda)=\inf \sigma^{*} (f,\lambda) ,$

то их общее значение называется двойным интегралом от по прямоугольнику и обозначается

$\displaystyle \iint\limits_{D}f= \iint\limits_{D}f (x,y) dxdy .$

Интеграл от функции по произвольному плоскому множеству $\Omega$ определяется равенством

$\displaystyle \iint\limits_{\Omega}f= \iint\limits_{D}f \chi_{\Omega} ,$

где $\chi_{\Omega}$ -- характеристическая функция множества $\Omega$ :

$\displaystyle \chi_{\Omega} (x,y)= \begin{cases}1 ,& (x,y)\in\Omega 0 ,& (x,y)\notin\Omega , \end{cases}$

а -- прямоугольник, содержащий $\Omega$ . Основные свойства двойного интеграла -- его линейность, аддитивность и монотонность:

$\displaystyle 1)$	$\displaystyle \quad\iint\limits_{\Omega} (\alpha f+\beta g)= \alpha\iint\limits_{\Omega} f+\beta \iint\limits_{\Omega}g\,,\qquad \alpha,\beta=Const\,,$
$\displaystyle 2)$	$\displaystyle \quad\iint\limits_{\Omega_{1}\cup\Omega_{2}}f= \iint\limits_{\Ome... ...f+ \iint\limits_{\Omega_{2}}f\,, \qquad \Omega_{1}\cap\Omega_{2}=\varnothing\,,$
$\displaystyle 3)$	$\displaystyle \quad f\leqslant g \quad \Rightarrow \quad \iint\limits_{\Omega}f \leqslant \iint\limits_{\Omega}g\,.$

Ответ: 2

Определим сначала тройной интеграл от функции по прямоугольному параллелепипеду (брусу) . Пусть $\lambda$ -- разбиение бруса, получающееся дроблением его ребер. Для ячейки разбиения $\lambda$ положим

$\displaystyle m_{A}=\inf_{A}f ,\qquad M_{A}=\sup_{A}f$

и введем нижнюю и верхнюю суммы Дарбу

$\displaystyle \sigma_{*} (f,\lambda)=\sum m_{A}V (A) ,\qquad \sigma^{*} (f,\lambda)=\sum M_{A}V (A) ,$

где -- объем ячейки . При продолжении разбиения нижняя сумма Дарбу $\sigma_{*}$ может лишь увеличиться, а верхняя -- лишь уменьшиться. Если

$\displaystyle \sup \sigma_{*} (f,\lambda)=\inf \sigma^{*} (f,\lambda) ,$

то их общее значение называется тройным интегралом от по брусу и обозначается

$\displaystyle \iiint\limits_{D}f= \iiint\limits_{D}f (x,y,z) dxdydz .$

Интеграл от функции по произвольному множеству $\Omega$ определяется равенством

$\displaystyle \iiint\limits_{\Omega}f= \iiint\limits_{D}f \chi_{\Omega} ,$

где $\chi_{\Omega}$ -- характеристическая функция множества $\Omega$ :

$\displaystyle \chi_{\Omega} (x,y)= \begin{cases}1 ,& (x,y)\in\Omega 0 ,& (x,y)\notin\Omega , \end{cases}$

а -- брус, содержащий $\Omega$ . Основные свойства тройного интеграла -- его линейность, аддитивность и монотонность:

$\displaystyle 1)$	$\displaystyle \quad\iiint\limits_{\Omega} (\alpha f+\beta g)= \alpha\iiint\limits_{\Omega} f+\beta \iiint\limits_{\Omega}g ,\qquad \alpha,\beta=Const ,$
$\displaystyle 2)$	$\displaystyle \quad\iiint\limits_{\Omega_{1}\cup\Omega_{2}}f= \iiint\limits_{\O... ...+ \iiint\limits_{\Omega_{2}}f , \qquad \Omega_{1}\cap\Omega_{2}=\varnothing ,$
$\displaystyle 3)$	$\displaystyle \quad f\leqslant g \quad \Rightarrow \quad \iiint\limits_{\Omega}f \leqslant \iiint\limits_{\Omega}g\,.$

Ответ:3

Сведение двукратного интеграла к повторному обеспечивается теоремой Фубини.

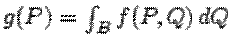Если -- функция, интегрируемая на $A\times B$ , где и -- брусы, и если при всех $P\in A$ функции переменной $Q\in B$ интегрируемы на , то функция $g (P)= \int_{B}f (P,Q) dQ$ интегрируема на , причем

$\displaystyle \;\iint\limits_{A\times B}f (P,Q)\,dPdQ= \int\limits_{A}dP \int\limits_{B}dQ\, f (P,Q)\,.$

Если область интегрирования функции не является брусом, для применения теоремы Фубини подынтегральную функцию продолжают нулем за пределы области и интегрируют продолженную функцию по любому брусу, содержащему исходную область интегрирования. Например, для цилиндрической области $\Omega$ вида

$\displaystyle \Omega=\{(x,y)\vert a\leqslant x\leqslant b , \; \varphi (x)\leqslant y\leqslant \psi (x)\}$

описанная процедура даст

$\displaystyle \iint\limits_{\Omega}f(x,y) dxdy= \int\limits_{a}^{b}dx \int\limits_{\varphi (x)}^{\psi (x)}dy f (x,y) .$

Ответ: 4

Аддитивная функция множества $\Phi (A)$ обладает тем свойством, что если $A_{1}\cap A_{2}=\varnothing$ , то

$\displaystyle \Phi (A_{1}\cup A_{2})=\Phi (A_{1})+\Phi (A_{2})\,.$

Будем рассматривать только регулярные аддитивные функции, т.е. такие, которые определены на жордановых множествах и обладают свойством

$\displaystyle V (A)=0 \quad \Rightarrow \quad \Phi (A)=0\,,$

где -- объем множества .

Плотность аддитивной функции $\varphi (P)$ это такая функция точки, значение которой в точке получается как следующий предел

$\displaystyle \varphi (P)= \lim_{n\to \infty} \frac{\Phi (A_{n})}{ V (A_{n})}\,,$

где $A_{n}$ последовательность множеств, стягивающаяся к точке , если этот предел не зависит от выбора последовательности $A_{n}$ . Стягивающаяся к точке последовательность состоит из жордановых множеств ненулевого объема, содержащих точку и с некоторого номера содержащихся в произвольно малой окрестности точки .

Если $\varphi$ -- непрерывная плотность аддитивной функции $\Phi$ , то сама аддитивная функция может быть восстановлена при помощи интегрирования:

$\displaystyle \Phi (A)= \int\limits_{A}\varphi (P)\,dP\,.$

Ответ: 5

Функция 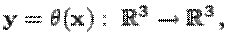$\mathbf{y}=\theta (\mathbf{x}) :\;\mathbb{R}^{3}\to \mathbb{R}^{3}\,,$ называется дифференцируемой в точке $\mathbf{x}$ , если

$\displaystyle \theta ( \mathbf{x}+ \mathbf{h})- \theta (\mathbf{x}) = \theta_{\... ... (\mathbf{h})+ o (\vert \mathbf{h}\vert)\,, \qquad \vert\mathbf{h}\vert\to 0\,,$

где $\theta_{ \mathbf{x}}'$ -- некоторое линейное отображение, называемое производной функции $\theta$ в точке $\mathbf{x}$ . Матрица этого отображения и называется матрицей Якоби. Столбцами ее служат векторы

$\displaystyle \frac{\partial\theta}{\partial x_{j}}= \begin{pmatrix}\frac{\part... ...y_{2}}{\partial x_{j}}\\ \frac{\partial y_{3}}{\partial x_{j}} \end{pmatrix}\,.$

Определитель матрицы Якоби называется якобинаном

$\displaystyle \det\theta'=\det \left( \frac{\partial y_{i}}{\partial x_{j}} \right)= \frac{D (y_{1}, y_{2}, y_{3})}{D (x_{1},x_{2},x_{3})}\,,$

это скалярная функция точки.

Матрица Якоби в точке $\mathbf{x}$ определяет главную линейную часть искажения при отображении $\theta$ бесконечно малого вектора с началом в точке $\mathbf{x}$ , тем самым она определяет линейную часть искажения бесконечно малого бруса, построенного на векторах с началом в точке $\mathbf{x}$ . Коэффициент искажения объема для такого бруса равен абсолютной величине якобиана отображения в этой точке (геометрический смысл).