Introduction to Quantum Electrodynamics, страница 4

The absorption of a photon can be considered in the same way as the emission. It can be shown that

                        .

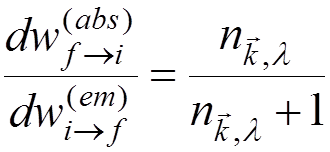         Bethe’s evaluation of the Lamb shift

      Electron self energy in non-relativistic 

                         approximation

We consider a non-relativistic H-like atom. The interaction of the atomic electron with the quantized radiation field in the electric-dipole approximation is described by the operator

                        .

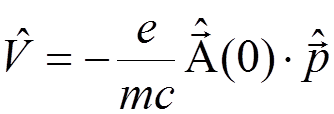Let us evaluate the    energy shift of atomic level  due to this interaction. To first order, one easily finds

                             .

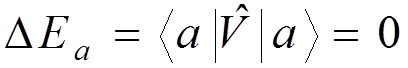To second order, we have (“self energy”)

                            

Using the standard replacement

                            ,

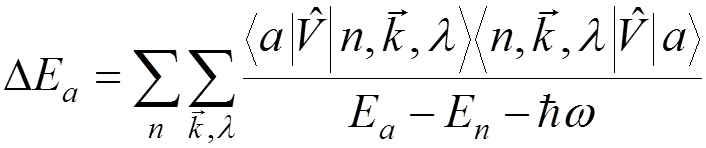
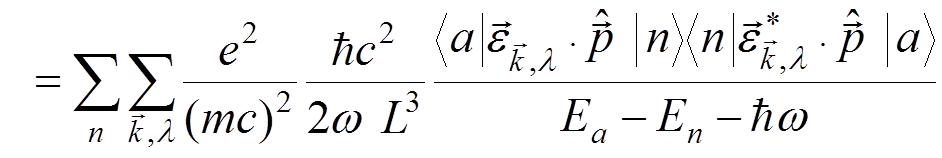
we obtain

  .

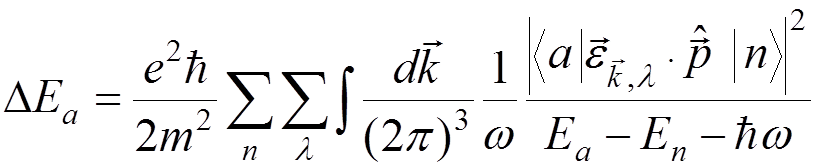The angular integration over photon momentum directions and the summation over photon polarization is performed by formula

 .

We obtain

 .

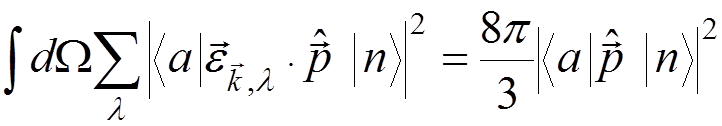Introducing  , we have

 .

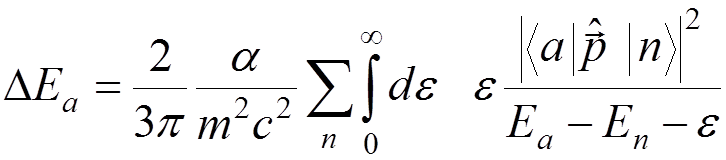This integral diverges linearly at high . However, we may argue that we can not take too seriously the contributions from virtual photons of energy

                                     ,

since our consideration is  non-relativistic. So, we replace

                                                ,

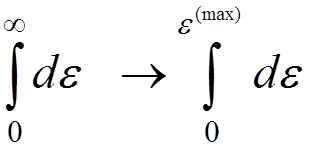where  .

                       Mass renormalization

Let us consider the self energy for a free non-relativistic electron. Taking into account that, for a free electron, non-diagonal matrix elements of   vanish,  we get

         ,

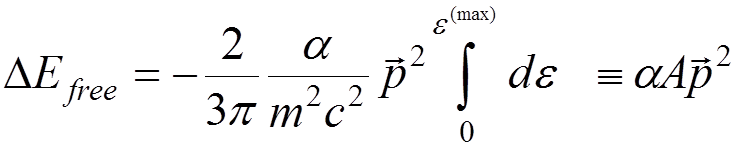where   is the momentum of the free electron. This integral is also linearly divergent as .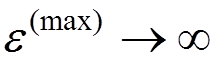

Since, we can not switch off the electromagnetic interaction, 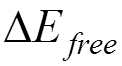 can not be separated from the usual kinetic energy. In fact, the observable kinetic energy is the sum of the kinetic energy of the bare electron

where  is the bare electron mass (the electromagnetic interaction is switched off) and .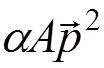

The observed (physical) electron mass is defined by

  .

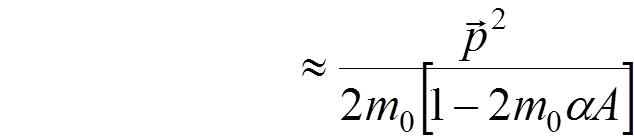It follows

            .

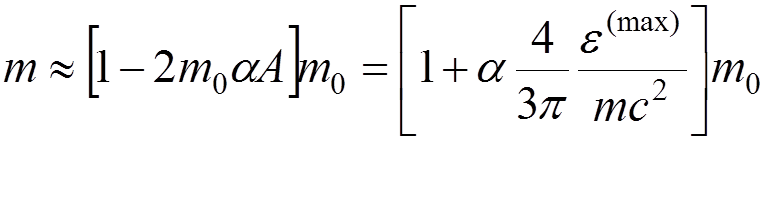       Let us now return to the atomic energy shift.

When we solve the Schroedinger equation, to find the unperturbed energy we use 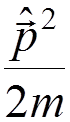  (which includes  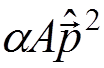 ) instead of   .

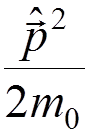Therefore, when we calculate the energy shift due to the interaction with the radiation field, we must subtract the term

                                            

to avoid any double accounting. In other words, we must use in the Schroedinger equation

 

        .

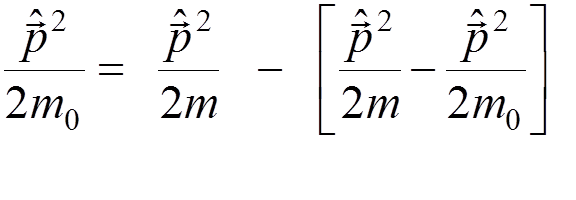
The observable energy shift is

.

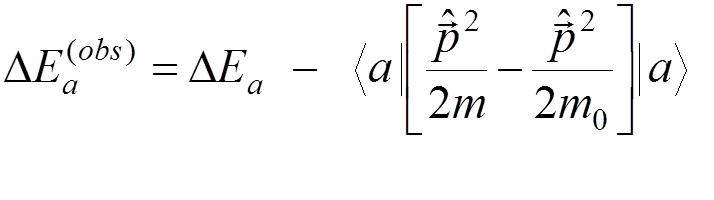
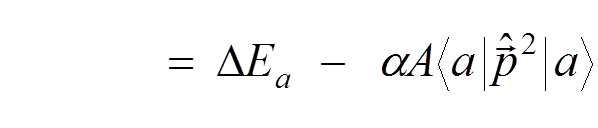In other words, what is observable is the difference of the bound-electron self energy and the free-electron self energy.

We have

Transforming

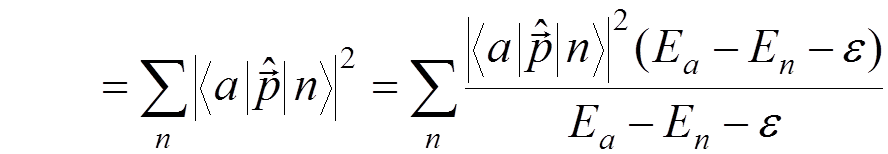
we obtain

              

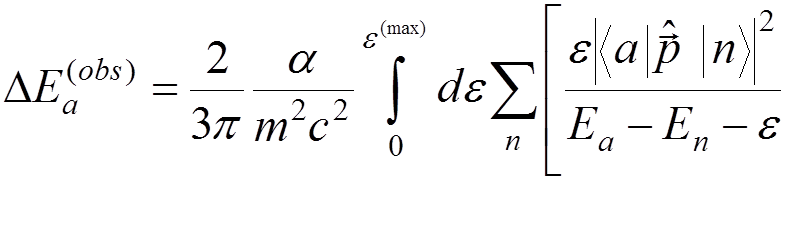
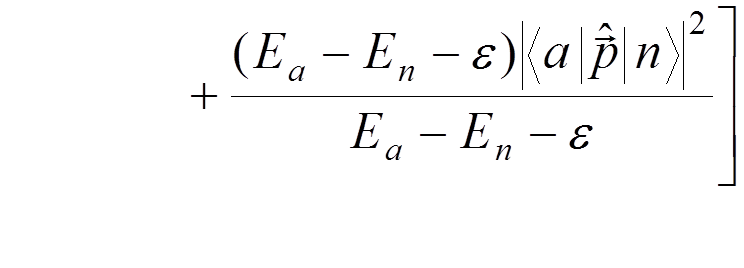
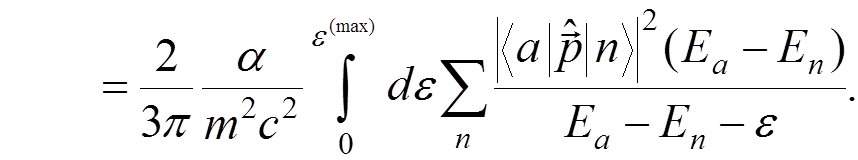
Taking into account that

           ,

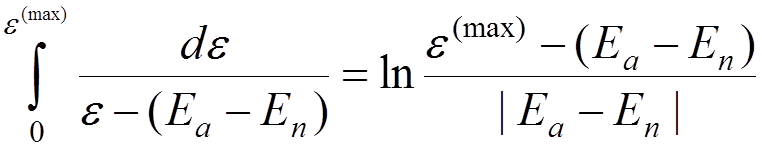
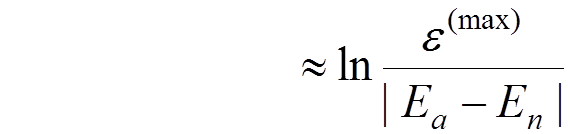we get

         .

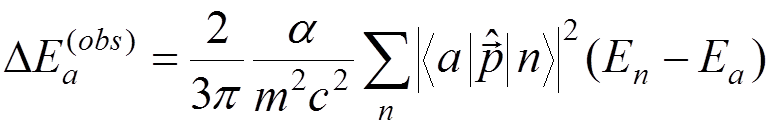
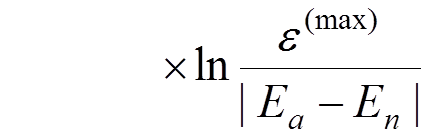This expression still diverges as 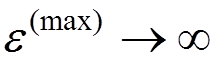 but the divergence is logarithmic. In the relativistic theory this divergence vanishes. We can obtain a good estimate for   by putting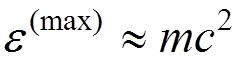  

  ( is not very sensitive to the choice o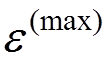f ,  if ).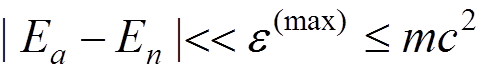

Finally, we obtain (Bethe, 1947)

         ,

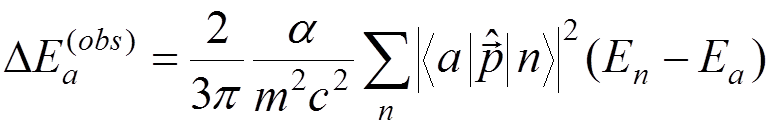
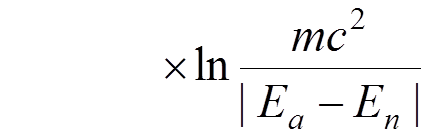or using

 ,

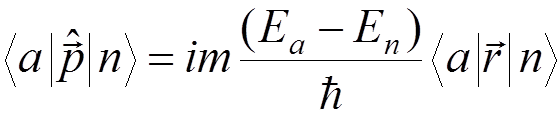we have

         .

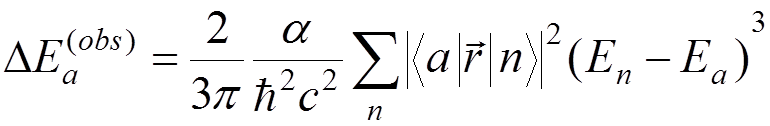
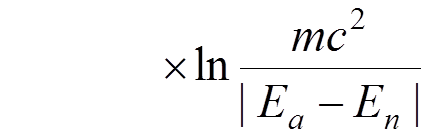The numerical evaluation of this term yields

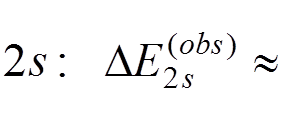             1040 MHz

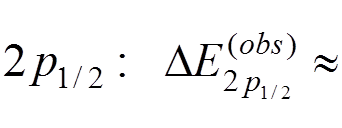             0

This energy splitting is in a good agreement with the first experiment by Lamb and Retherford (1947):

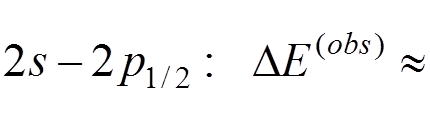             1062(5) MHz .         

Quantization of the electron-positron field

In relativistic quantum mechanics the one-electron atom is described by the Dirac equation

                  ,

where

             .

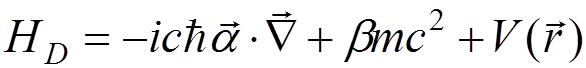To formulate a consequent relativistic theory of  electrons and positrons, we must quantize the Dirac field

 ,

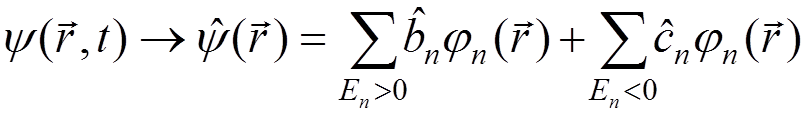where 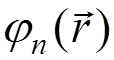   are  solutions of the stationary Dirac equation