Non-relativistic
\ ![]()
![]()
![]() theory \
F=1
theory \
F=1
![]()
![]()
![]() \
\ ![]() /
F=0
/
F=0
\______________/
Lamb Hyperfine
Fine structure shift splitting
splitting
Quantization of the free electromagnetic
field
Classical free electromagnetic fields are described by the Maxwell equations
 ,
, 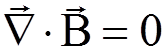 ,
,
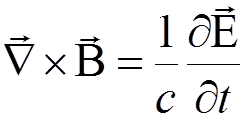 ,
, 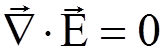 .
.
![]() and
and ![]() are conveniently expressed in terms of the
scalar and vector potentials:
are conveniently expressed in terms of the
scalar and vector potentials:
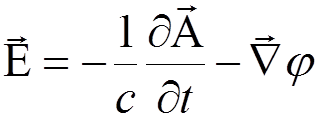 ,
,
 .
.
The
potentials ![]() and
and ![]() are not
unique quantities. They admit the following transformation
are not
unique quantities. They admit the following transformation
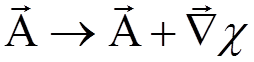 ,
, 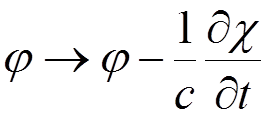 ,
,
which is known as a gauge transformation.
In what follows, we will use the Colomb gauge:
 .
.
In this
gauge, ![]() can be chosen to vanish:
can be chosen to vanish:
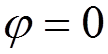 .
.
Then, the second couple of the Maxwell equations takes the form
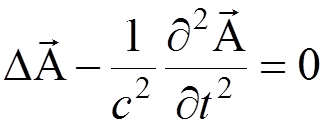 ,
,
while the first couple is satisfied automatically if the representation in terms of the vector and scalar potentials is employed.
Radiation field as a collection of harmonic
oscillators
We
assume the periodic boundary conditions for![]()
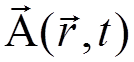 enclosed in a box with
enclosed in a box with  . Remembering the reality of
. Remembering the reality of ![]() , we can write the Fourier
decomposition in the form
, we can write the Fourier
decomposition in the form
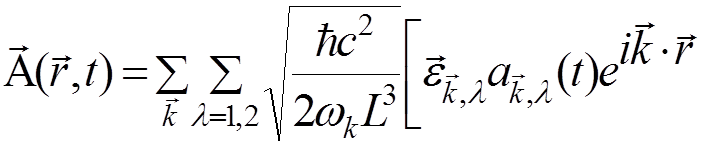
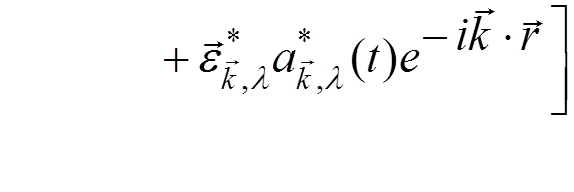 ,
,
where 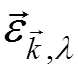 are the polarization vectors and
are the polarization vectors and 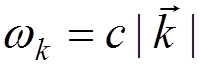 . The polarization vectors obey the
transversality condition
. The polarization vectors obey the
transversality condition
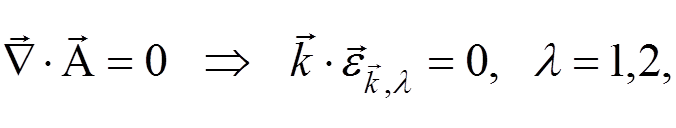
the
ortogonality condition 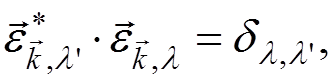 and the
completeness condition
and the
completeness condition
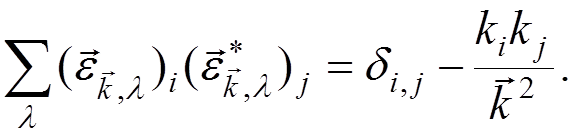
Substituting
the Fourier decomposition of 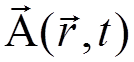
into the Maxwell equation, we obtain
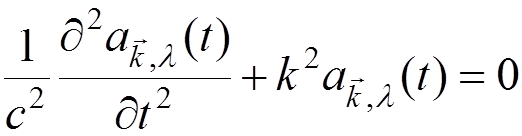
or
 .
.
This means that the radiation field can be regarded as a collection of independent harmonic oscillators.
The energy of the radiation field:
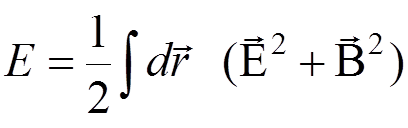 .
.
Substituting 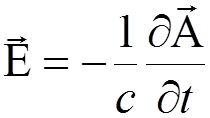 and
and  into
this equation and using the Fourier decomposition of
into
this equation and using the Fourier decomposition of 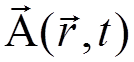 given
above, we obtain
given
above, we obtain
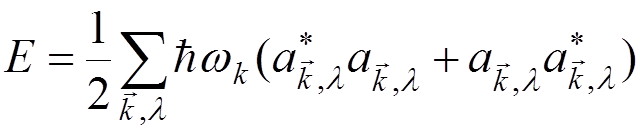 .
.
Thus, the energy of the radiation field is the sum of the energies of the harmonic oscillators.
So far, we considered classical fields. To pass to the quantum theory of the radiation field, we must quantize the radiation harmonic oscillators according to the procedure we learnt from non-relativistic quantum mechanics.
Harmonic oscillator
In classical physics, the harmonic oscillator is described
by the Hamiltonian
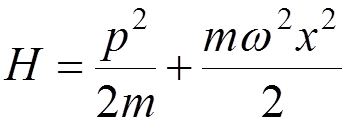 .
.
In variables
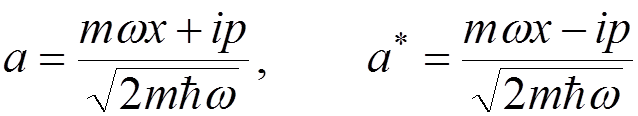 ,
,
it takes the form
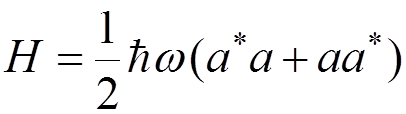 .
.
To pass to the
quantum theory, we replace the classical quantities 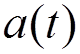 and
and  by so-called annihilation (
by so-called annihilation (![]() ) and creation (
) and creation (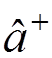 )
operators for a quant of energy
)
operators for a quant of energy ![]() .
.
In the usual
(Schroedinger) representation, the operators do not depend on time. The time
dependence is determined by the wave function. The operators ![]() and
and 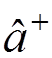 obey
the following commutation relations
obey
the following commutation relations
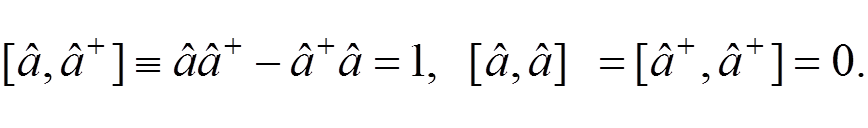 The classical Hamiltonian
The classical Hamiltonian ![]() is replaced by the energy operator
is replaced by the energy operator
 .
.
Using the commutation relations, we obtain
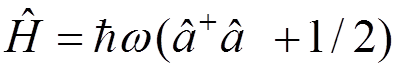 .
.
A state defined by
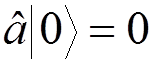
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.