is an eigenstate of
![]() with eigenvalue
with eigenvalue ![]() :
:
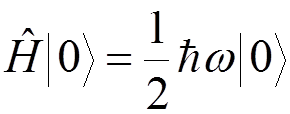 .
.
Using the commutation relations

one finds that the states
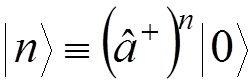
are eigenstates of ![]() with eigenvalues
with eigenvalues
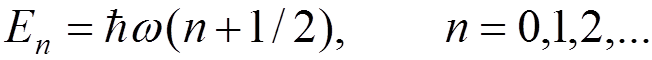
These states exhaust
the spectrum of ![]() . The operator
. The operator
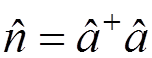
is known as the
occupation number operator . Its eigenvalues are 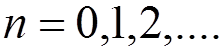
Explicit matrix
representations of ![]() ,
,  , and
, and ![]()
consistent with the commutation relations are
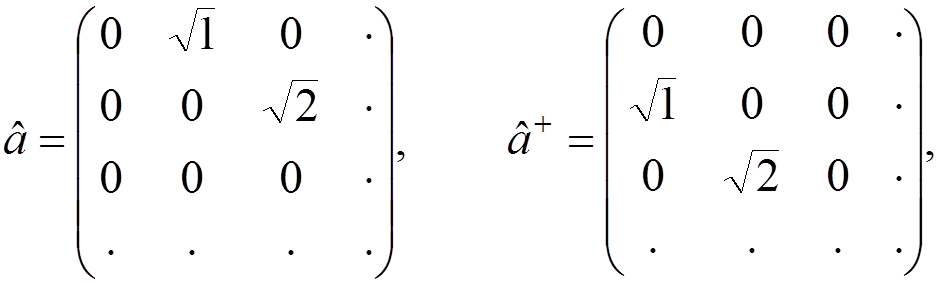
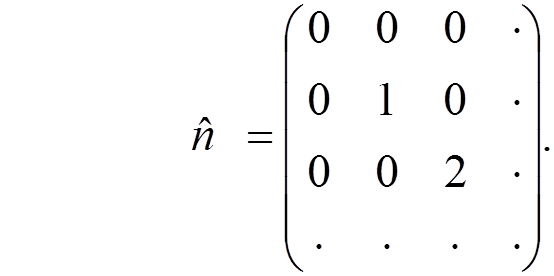
They are assumed to act on a column vector represented by
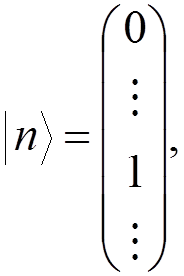
where only the 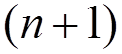 entry is different from zero.
entry is different from zero.
Quantization of the radiation field
We replace  and
and 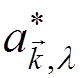 by the
annihilation and creation operators:
by the
annihilation and creation operators:

and postulate the following commutation relations
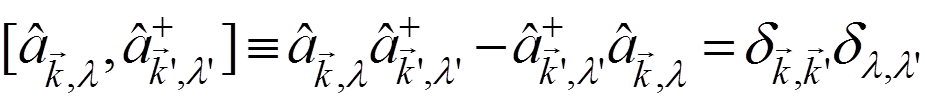
 .
.
The operators 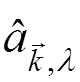 and
and 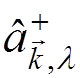 are
time-independent. The time dependence is determined by the wave function
are
time-independent. The time dependence is determined by the wave function
(the Schroedinger representation).
The vector potential operator
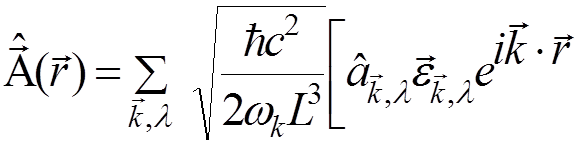
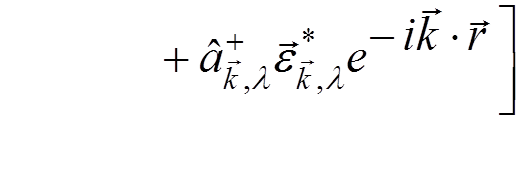 .
.
The
fields ![]() and
and ![]() are
also replaced by operators
are
also replaced by operators
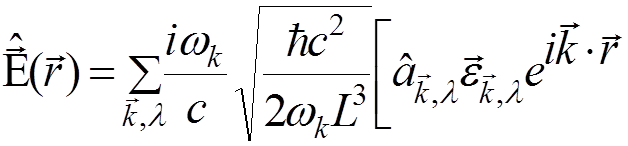
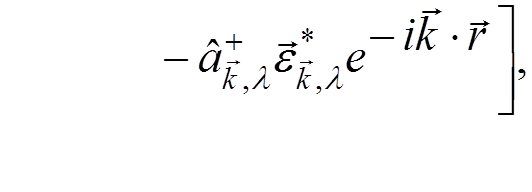
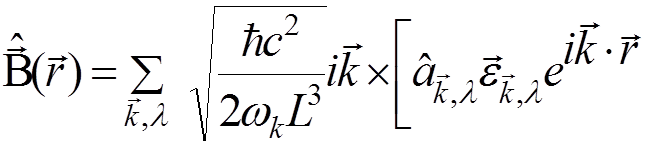
 .
.
The energy operator:
 .
.
Taking into account the commutation relation
 ,
,
we have
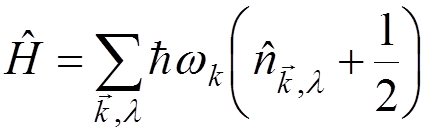 ,
,
where
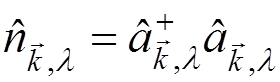
![]()
is the occupation number operator, which has eigenvalues
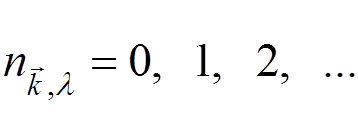
![]()
Let 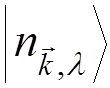 is a state with
is a state with 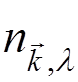 photons
of energy
photons
of energy 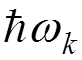 , momentum
, momentum  , and
polarization
, and
polarization ![]() . Using the commutation relations
for
. Using the commutation relations
for 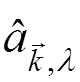 and
and  , one
finds
, one
finds
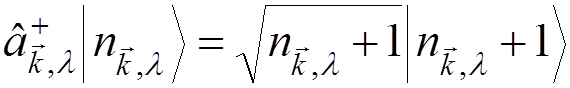 ,
,
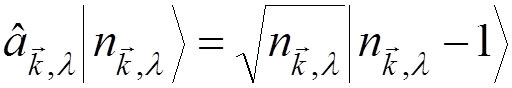 ,
,
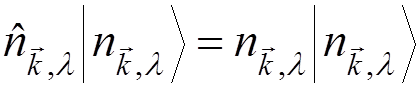 .
.
Non-zero matrix
elements of 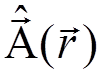 :
:
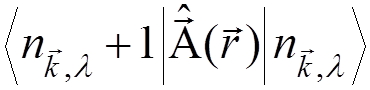
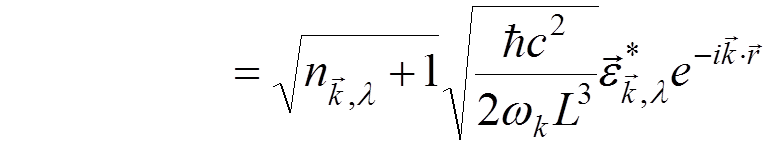
![]()
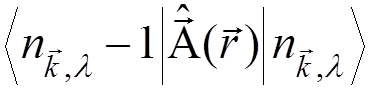
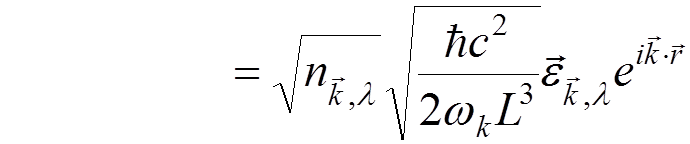
Emission and absorption of photons by atoms
Let us
consider a transition of a non-relativistic atom from state ![]() to state
to state 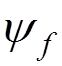 via
emission of a photon with energy
via
emission of a photon with energy ![]()
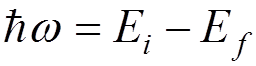 ,
momentum
,
momentum  , and polarization
, and polarization 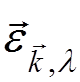 . For the system “atom + radiation field”,
this is a transition from the state
. For the system “atom + radiation field”,
this is a transition from the state 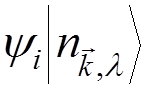 to
the state
to
the state 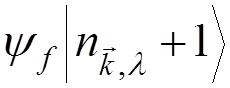 due to the interaction
due to the interaction
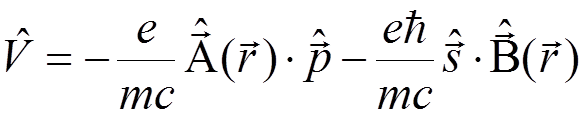 ,
,
where  is the electron momentum operator and
is the electron momentum operator and ![]() is the electron spin operator.
is the electron spin operator.
Consider first the transition due to the term
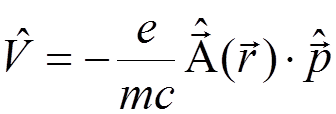 .
.
According to the general prescription of quantum mechanics, the transition probability per unit time into a
wave
vector element  is (the Golden Rule)
is (the Golden Rule)

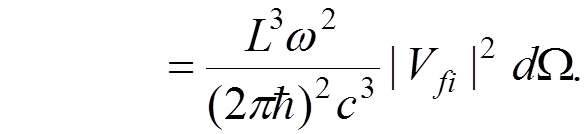
We have to evaluate
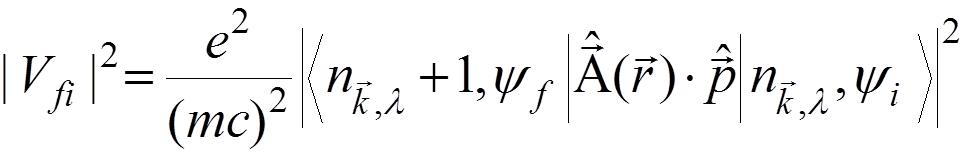
Because for a non-relativistic atom
 ,
,
in the
operator 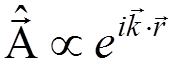 , we can replace
, we can replace
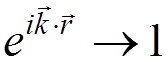 .
.
It yields
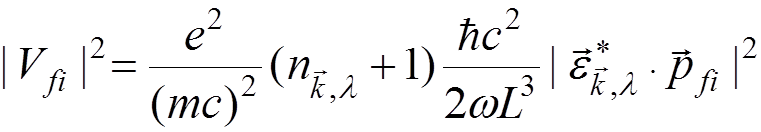 ,
,
where
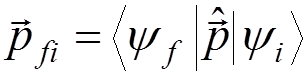 .
.
Transforming
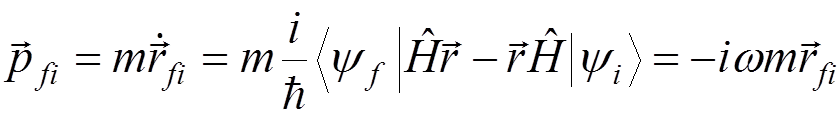 ,
,
we obtain
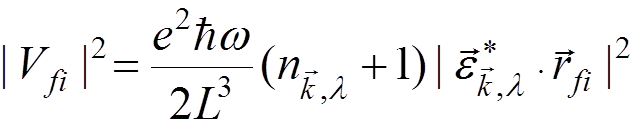 .
.
It gives
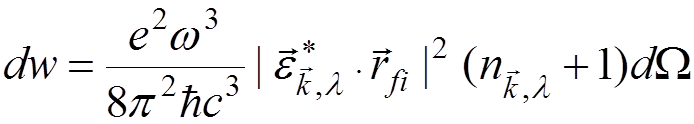 .
.
In the
expression 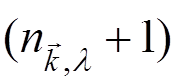 , the first term
, the first term ![]()
 corresponds to the induced emission while the second term
corresponds to the induced emission while the second term
 corresponds to the spontaneous emission.
corresponds to the spontaneous emission.
We note
that in the approximation used the matrix element 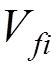 can be
represented as the matrix element of the operator
can be
represented as the matrix element of the operator
 .
.
For this reason, this transition is known as the electric dipole transition, E1.
The
total transition probability is obtained by integration over ![]() and summing over photon polarization. For
the spontaneous emission, one finds
and summing over photon polarization. For
the spontaneous emission, one finds
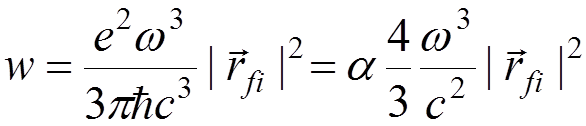 .
.
The selection rules for the electric dipole transition:
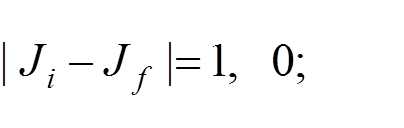 NO:
NO: ![]()
Parity change: YES
To the
next order in ![]() , the M1 and E2 transitions occur. The M1 transition is
determined by the operator
, the M1 and E2 transitions occur. The M1 transition is
determined by the operator
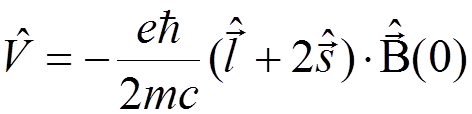 .
.
For an
H-like ion, its amplitude is smaller by factor ![]() than
the E1 amplitude.
than
the E1 amplitude.
The selection rules for the magnetic dipole transition:
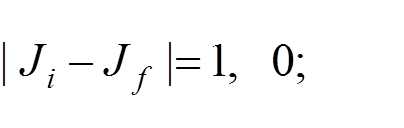 NO:
NO: ![]()
Parity change: NO
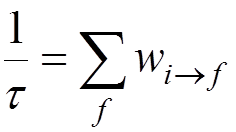 .
.
Absorption of a photon
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.