Расчет элементов металлоконструкций на статическое и динамическое нагружение, страница 12

2. Демонстрация форм колебаний

2.1. Первая форма колебаний

Первая форма колебаний; колебания происходят вдоль оси k с частотой собственных колебаний W=1,114 Гц. Наблюдается изгиб – половина волны синусоиды.

2.2. Вторая форма колебаний

Вторая форма колебаний. Колебания происходят вдоль оси k с частотой собственных колебаний W=2,039 Гц. Сильный изгиб испытывают центральный части ферменной конструкции, полная волна синусоиды, дополнительно изгиб колонн и частичный сдвиг.

Рис. 20. Вторая форма колебаний. Вид сверху. W=1,643 Гц.

Рис. 21. Вторая форма колебаний. Общий вид. W=1,643 Гц.

2.3. Третья форма колебаний

Третья форма колебаний. Колебания происходят вдоль оси i с частотой собственных колебаний W=2,039 Гц. Колебания затрагивают в основном несущие части конструкции (колонны).

Рис. 22. Третья форма колебаний. Вид сверху. W=2,039 Гц.

Рис. 23. Третья форма колебаний. Общий вид. W=2,039 Гц.

2.4. Четвертая форма колебаний

Четвертая форма колебаний. Колобания происходят вдоль оси k с частотой собственных колебаний W=2,039 Гц.

2.5. Пятая форма колебаний

Пятая форма колебаний. Колебания происходят вдоль оси i и k с частотой собственных колебаний W=2,039 Гц. Наблюдается одновременное действие крутящего и изгибающего моментов. Происходит поворот конструкции вокруг оси j, элементы как изгибаются, так и закручиваются.

Рис. 25. Пятая форма колебаний. Вид сверху. W=2,824 Гц.

Рис. 26. Пятая форма колебаний. Общий вид. W=2,824 Гц.

Раздел III. Моделирование отклика на сейсмическое воздействие

3.1. Метод прямого интегрирования (метод Ньюмарка)

При прямом интегрировании уравнение

решается с помощью численной пошаговой процедуры. Термин «прямое» говорит о том, что не проводится никаких предварительных преобразований уравнений динамического равновесия. Решение ведется по шагам, на каждом шаге, по существу, решается статическая задача. Равновесие с учетом сил демпфирования и инерции рассматривается в дискретных точках временного интервала. Таким образом, для конкретного момента времени τ решается задача

                                              {I}

где ,  – так называемые, эффективные матрица жесткости и вектор нагрузок. Выражение {1} служит для определения вектора обобщенных перемещений {q} в рассматриваемый момент времени τ.

Методы прямого интегрирования различаются способами интерполяции или экстраполяции перемещений на каждом достаточно малом временном интервале.

3.2. Метод Ньюмарка

Метод Ньюмарка, называемый также методом обобщенного ускорения, использует следующие предположения:

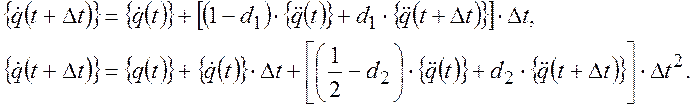                        (II)

Здесь dl, d2 – параметры интегрирования. При d1=0,5; d2=0,25 эти соотношения будут отвечать предположению о постоянном характере ускорения на временном интервале. При d1=0,5; d2=1/6 – о линейном изменении ускорения, что аналогично методу Вилсона при θ=1. При d2=0 получим центрально-разностную схему вычислений, соответствующую двойной пульсации ускорения в начале и конце каждого временного интервала. Таким образом, d2 определяет закон изменения ускорения в пределах шага счета.

Параметр dl характеризует схемное (численное) демпфирование: при 0<dl<0,5 – отрицательное, при dl>0,5 – положительное, при dl=0,5 схемное затухание отсутствует.

При решении конечномерных задач большой размерности рекомендуется принимать dl>0,5; d2>0,25.