Расчет элементов металлоконструкций на статическое и динамическое нагружение, страница 11

Поперечные сечения подбирались с таким учетом, чтобы не превышали допускаемого равного 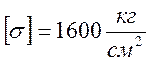 и запас по устойчивости отношение 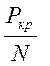было по абсолютному значению больше единицы.

В виду этого максимальные напряжения наблюдаются в 7 и 14 конечных  элементах составляют 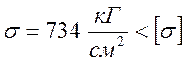 , запас по устойчивости =3,63 , стержни работают на сжатие. Был взят профиль гнутый замкнутый электросварной и выбирался в соответствии с ГОСТ 30245-94. Для внешних стержней 50х50х2,5; для внутренних 50х50х2.

В результате сравнения веса фермы и несущей балки из составного сечения заключаем, что использование фермы конструктивно выгоднее.

В третьем разделе была рассчитана несущая способность панели, которая равна при сжатии- 10564 кг. При достижении данного предела нагружения наступает местная потеря устойчивости пластинок между стрингерами (образование вмятин), затем – общая потеря устойчивости всей панели.

При попытке повысить несущую способность панели с помощью увеличения толщины листа в результате получили увеличение веса балки, весьма значительное. Поэтому более эффективным с точки зрения предъявляемых технологических требований повышать несущую способность панели при сжатии более целесообразно используя подкрепляющие ребра.

            Таким образом, если в конструкции будут использоваться колонны с составным сечением, ферменные конструкции и панели усиленные подкрепляющими ребрами, то будет достигнута максимально возможная экономия, легкость конструкции, достаточная прочность и запас по устойчивости, при данных пределах нагружения.

Часть II. Расчет металлоконструкций на сейсмическое воздействие

Введение

Исходя из проделанных расчетов в части I данной работы, смоделируем металлоконструкцию. Для этой модели определим собственные частоты и моды колебаний методом обратных итераций, рассчитаем отклик системы на сейсмическое воздействие методом прямого интегрирования (методом Нююмарка). Алгоритм решения заложен в программах :

·  Stud03.exe;

·  Sob2so3.exe;

·  Dinams.exe;

·  Argus.exe.

Раздел I. Построение металлоконструкции

1.Расчет несущей пролетной балки

Рис.12. Пролетная планка

p - снеговая нагрузка, L=b – длина пролета,

Осуществим подбор поперечного сечения несущей пролетной балки по схеме:

·  возьмем швеллер №33

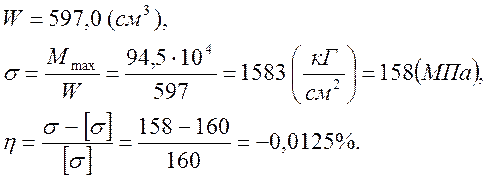
Моменты инерции сечения:

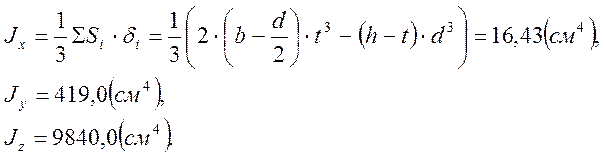
2.Расчетная схема конструкции

Рис.13. Общий вид модели

Рис.14. Главный вид модели

Рис.15. Вид модели сверху

Рис.16. Вид модели сбоку

Данная модель состоит из 189 конечных элементов;

задано 618 степеней свободы.

Вес смоделированной конструкции – 6033 кг.

Раздел II. Расчет низших собственных частот и мод колебаний

1. Метод обратных итераций

Если требуется для матриц большого размера [K], [M] найти лишь несколько собственных значений вместе с соответствующими собственными векторами, то наиболее эффективным путем решения задачи становятся степенные методы, разделяющиеся на методы прямых и обратных итераций.

Метод обратных итераций может быть сформулирован следующим образом:

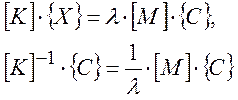
В методе обратных итераций вычисляется последовательность векторов {x}_k, начальный вектор {e} – произвольный. Вектор {x} ищется из решения уравнения:

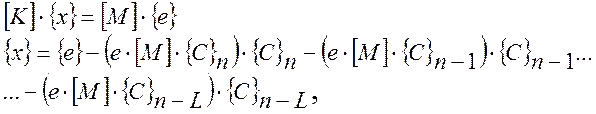
где {e} –произвольный вектор, ортогонален по матрице масс [M] к каждому из известных собственных векторов {C}_i.

Вычислительный процесс, реализующий метод обратных итераций, сходится к наименьшему собственному значению λ_i и соответствующему собственному вектору {C}_i.

Для ускорения сходимости рассмотренных итерационных методов применяются сдвиги. Пусть {λ_i} – множество собственных значений задачи. Рассмотрим следующую проблему собственных значений:

.

Собственные числа нестандартной задачи {λ}’ связаны с {λ_i} соотношением λ_i’= λ_i-σ, где σ – любое вещественное число, называемое сдвигом. Собственные вектора {c’}_i и {c}_i , совпадают. Введя сдвиг σ и сформировав матрицу [K]’×{C}=l’×[M]×{C}, используя при решении которой степенные методы, определяют или наиболее удаленные от s значения l_i для исходной задачи (метод прямых итераций) или ближайшие к s l_i  (метод обратных итераций).