





2. Сведения из теории
2.1 НАПРЯЖЕННО-ДЕФОРМИРОВАННОЕ СОСТОЯНИЕ СПЛОШНОЙ СРЕДЫ
Существует обширный класс задач, в которых эффектами инерции и взаимосвязи тепловых и механических процессов можно пренебречь. Тогда совместная задача термоупругости образует две раздельные задачи, решение которых выполняются последовательно и независимо.
Основные уравнения такой несвязанной задачи нестационарной термоупругости /без учёта теплообразования при деформации, но с учётом переноса координат/ в квазистатической постановке по напряженному состоянию следующие:
а/ уравнение теплопроводности
КТ,ii =rcv![]() , (2,1)
, (2,1)
б/ уравнение равновесия
sij,j + rbi=0, (2,2)
в/ уравнения связи тензоров напряжений и деформации
sij =ld ijekk + 2meij –(3l+2m)ad ije(T-T0), (2,3)
г/ уравнение связи деформаций с перемещениями
eij=0.5(ui,j + uj,i ) , (2,4)
Дополняя последние три уравнения (2.1-2.4) задачи теории упругости различными краевыми условиями на поверхности ограничивающей рассматриваемое тело получаем полный набор соотношений, характеризующих напряженно-деформированное состояние среды.
2.2 ПЕРЕХОД ОТ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
К РАСЧЕТНОЙ МОДЕЛИ СОСТОЯНИЯ СРЕДЫ
Процессы деформирования среды связаны с изменением её температурного состояния и наоборот, - изменение температуры среды создаёт её деформацию. В целом это диктует целесообразность решения связанной задачи теплового и деформированного состояний как это принято при теоретическом подходе. Унификация же программных разработок предполагает условия полного алгоритмического решения частных задач - теплового и напряженно-деформированного состояний среды, а затем их последующего объединения. При этом каждое дифференциальное уравнение, представленные ранее, необходимо изложить применительно к некоей абстрактной модели, наделенной всевозможными вариантами описываемого им явления. Этот переход требует некоторых навыков рассмотрения обычного физического явления, что вызвано потребностью универсальности алгоритма решения. К примеру, среда может состоять из разнородных фрагментов, имеющих различные свойства. Область пространства, ограниченного средой может иметь незамкнутую поверхность в разных частях. Таким образом, часть среды можно считать полупространством. Кроме того, на поверхность тела возможно воздействие однотипных проявлений, но происходящих в разных ее местах.
Ниже излагается описание наиболее полной абстрактной модели, позволяющей выполнять такой переход.
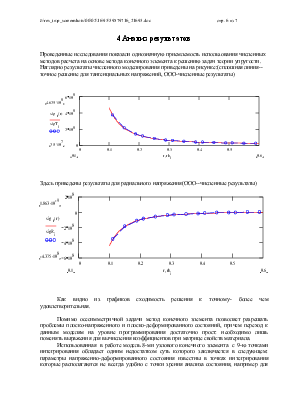
Рис.1 Тело, представленное набором элементарных
объемов и поверхностей 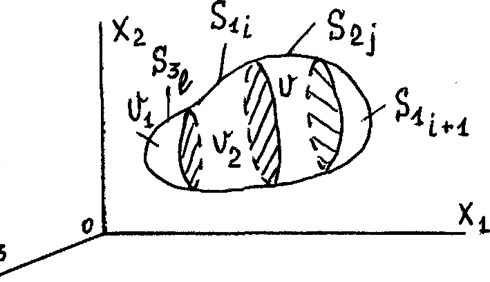
X3
Тело, объёмом V ограниченное поверхностью S /рис.1/ при его дискретном представлении состоит из К элементов объёма и I, J, L, M,… частей поверхности (количество которых может быть разным в разных задачах):
V=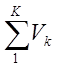 , S=
, S=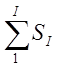 +
+ 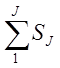 +
+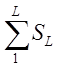 +…+
+…+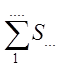 .
.
При этом в задаче динамического поведения каждый элемент объёма тела VK обладает конкретными физико-механическими свойствами:
- модулями упругости EVk,GVkпервого и второго рода (МПа) для изотропного тела и дополнительными, характеристиками упругости для анизотропного;
-
плотностью ![]() (кг/см3).
(кг/см3).
Кроме того, на каждую частицу тела может действовать массовая сила qV , вызванная силами тяжести при действии перегрузок с коэффициентом ng, либо электромагнитными полями в объёмеV, либо его части;
На
поверхности S1
действует нагрузка интенсивностью qj(t)
(МПа), на S2 возможны кинематические
перемещения, переменные или изменяемые во времени uJ(t) (см) и на
поверхности S3
перемещения uL(t) и скорость
![]() (см/сек)
характер изменения которых во времени известен. Дополнительно, на элементарных
поверхностях S4 действуют
сосредоточенные силы pm .
(см/сек)
характер изменения которых во времени известен. Дополнительно, на элементарных
поверхностях S4 действуют
сосредоточенные силы pm .
Для произвольного момента времени процесс динамического нагружения конструкции описывается системой обыкновенных дифференциальных уравнений второго порядка
M![]() +С
+С![]() + КU
= F (1.5)
+ КU
= F (1.5)
Чаще всего матрицей демпфирующих свойств, в предварительном расчете пренебрегают, поэтому уравнения на это слагаемое сократим
M![]() + КU = F . (1.5а)
+ КU = F . (1.5а)
Тогда, с учетом сказанного,
[М]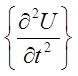 + [C]{U} ={Fqv}V+{
+ [C]{U} ={Fqv}V+{![]() }V +{Fq}S1+{pm}S4 ,
}V +{Fq}S1+{pm}S4 ,
при
{uJ(t)}S2 наS2 и {uL(t)}S3 и {![]() }S3 наS3 .
}S3 наS3 .
где: [M], M - матрица распределения плотности и матрица жесткости [К], К ;
{Fqv}Vи {![]() }V -
векторы нагрузок, вызванные массовыми силами и действием неравномерного
теплового поля {DT}v, вследствие деформации {eo}v линейного расширения; {Fq}S1, поверхностными
на S1 и локальными {pm}S4 на S4. Кинематические
ограничения, накладываемые на поверхности наS2 нS3 определяются
векторами {uJ(t)}S2 наS2 и {uL(t)}S3, {
}V -
векторы нагрузок, вызванные массовыми силами и действием неравномерного
теплового поля {DT}v, вследствие деформации {eo}v линейного расширения; {Fq}S1, поверхностными
на S1 и локальными {pm}S4 на S4. Кинематические
ограничения, накладываемые на поверхности наS2 нS3 определяются
векторами {uJ(t)}S2 наS2 и {uL(t)}S3, {![]() }S3 . Размерность
решаемой системы (n, nx2, nx3) зависит от вида
описания пространства, и изменяется пропорционально ему.
}S3 . Размерность
решаемой системы (n, nx2, nx3) зависит от вида
описания пространства, и изменяется пропорционально ему.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.