Напряженно-деформированное состояние сплошной среды. Функции формы квадратичных элементов, страница 3

 Вычисление матрицы механических свойств области (программой предусмотренно задание подобластей с различными механическими свойствами )

Определение координат текущего конечного элемента в общей (глобальной) системе

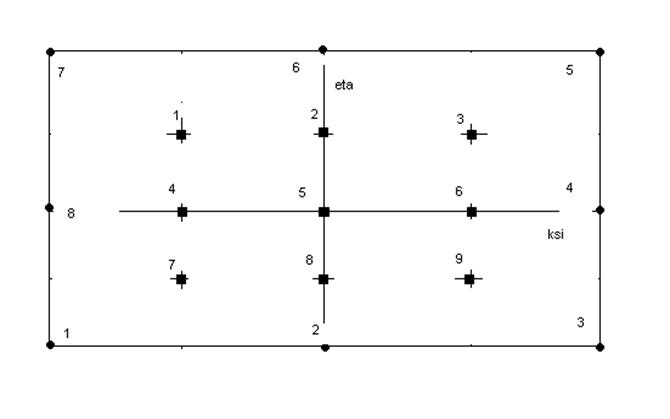
        4.1 Цикл по точкам интегрирования (каждый конечный элемент имеет 9 точек            

 интегрирования)

        4.2 Вычисление значений производных от функций формы (по значениям локальных координат текущей точки интегрирования)

        4.3 Вычисление значений функций формы (по значениям локальных координат текущей точки интегрирования)

        4.4 Вычисление Якобиана

        4.5 Вычисление матрицы обратной Якобиану

        4.6 Вычисление определителя Якобиана

        4.7 Осуществление перехода от значений производных по локальным функциям формы  

              к соответствующим глобальным значениям градиентов посредством матрицы                 

               обратной Якобиану

        4.8 Перемножение полученных матриц градиентов с матрицей механических свойств

              в соответствующем порядке и, соответственно, получение некорректированного   

              вклада от каждой точки интегрирования в общую матрицу жесткости текущего

              конечного элемента

       4.9 Осуществление процедуры численного интегрирования  по объему (производится      

              суммированием полученных матриц жесткости от каждой точки интегрирования

              с домножением на соответствующие коэффициенты, текущий радиус точки                 

              интегрирования, определитель Якобиана)

       5.0 Конец цикла 4.1

5.1 Определение глобальных коэффициентов жесткости посредством индексного суммирования соответствующих коэффициентов жесткости текущих элементов

6.0 Конец цикла 4.0

7.0 Конец

Далее программа определяет вектор нагрузки, причем для полного соответсвия схеме решения, грань конечного элемента испытывающая давление, представляется стержневым   элементом имеющим 3 точки интегрирования и 6 степеней свободы.

Полученная система линейных уравнений решается с помощью процедуры LSLSFиз библиотеки математического обеспечения MSIMSL, стандартно входящей в пакет MicrosoftFortranPowerStation 4.0 .

Затем, используя определенные ранее, матрицы градиентов, осуществляется переход от полученных решением системы  линейных уравнений  перемещений к деформациям, и, далее от деформаций, посредством определенных ранее, матриц механических свойств конечных элементов, к напряжениям. 

Точное решение задачи толстого цилиндра и результаты численного моделирования предоставлены в приложении.    

4.Анализ результатов

Проведенные исследования показали однозначную приемлемость использования численных методов расчета на основе метода конечного элемента к решению задач теории упругости.

Наглядно результаты численного моделирования приведены на рисунке:(сплошная линия--точное решение для тангенциальных напряжений, ООО-численные результаты)

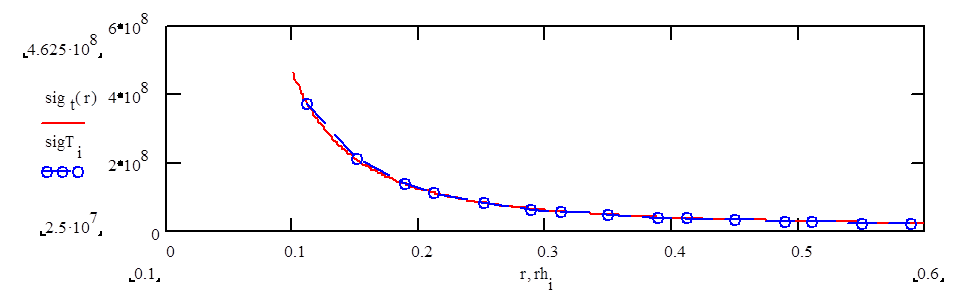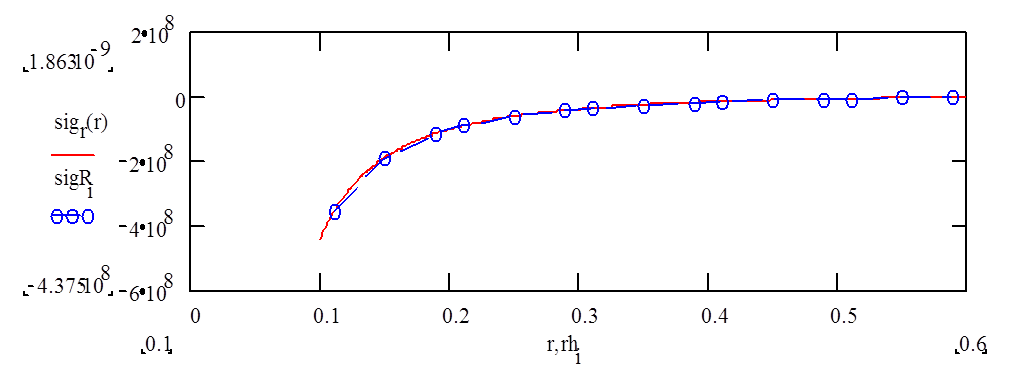
Здесь приведены результаты для радиального напряжения(ООО--численные результаты)

Как видно из графиков сходимость решения к точному- более чем удовлетворительная.

Помимо осесимметричной задачи метод конечного элемента позволяет разрешать проблемы плоско-напряженного и плоско-деформированного состояний, причем переход к данным моделям на уровне программирования достаточно прост: необходимо лишь поменять выражения для вычисления коэффициентов при матрице свойств материала.

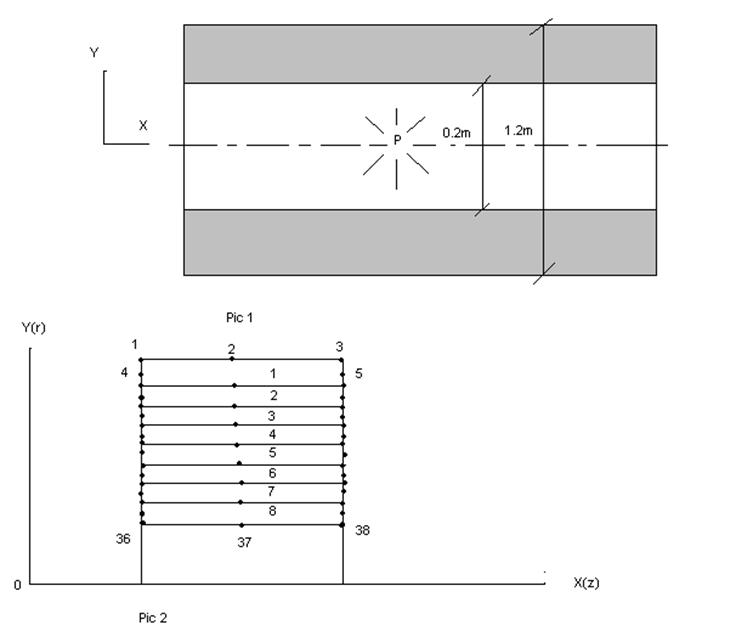
Использованная  в работе модель 8-ми узлового конечного элемента  с 9-ю точками интегрирования обладает одним недостатком суть которого заключается в следующем: параметры напряженно-деформированного состояния известны в точках интегрирования которые располагаются не всегда удобно с точки зрения анализа состояния, например для отслеживания  связи с граничными  условиями, часто необходимо располагать значениями определяемых величин на границах конечного элемента, которые существенно отстоят от точек интегрирования, поэтому приходится дополнительно аппроксимировать зависимость искомых параметров по местной системе координат внутри конечного элемента, для получения значений на границе конечного элемента. Но в данной работе такие исследования не проводились, так как целью работы было определение принципиальной возможности применения численных методов на основе конечного элемента.