Расчет конструктивных элементов на ползучесть

     БАЛТИЙСКИЙ  ГОСУДАРСТВЕННЫЙ

ТЕХНИЧЕСКИЙ  УНИВЕРСИТЕТ

«ВОЕНМЕХ» имени Д.Ф. Устинова

────────────────────────────────────

КАФЕДРА МЕХАНИКИ ДЕФОРМИРУЕМОГО

 ТВЕРДОГО ТЕЛА

 

РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА

Тема: «Расчет конструктивных элементов на ползучесть»

                                                                                 Преподаватель: Сухарев М.Г.

                                                                       Студент: Бертова А.В. 

                                                                        Группа: М-501

Санкт-Петербург

2003г.

1. Формулировка задания для прямоугольного сечения

Балка прямоугольного сечения h = 4 см, b = 2 см, l = 50 см, шарнирно закрепленная и нагруженная силами по концам величиной P = 4 кН. При температуре T = 500 °С. Материал – углеродистая сталь, коэффициент упругости Е = 1,6*10⁶ кГ/мм² , n = 3, k = 1,5 *10^-15 (см²/кГ)ⁿ *1/час.

Определить:

1) распределение нормальных напряжений по высоте балки, пренебрегая неустановившейся ползучестью;

2) наибольший прогиб через десять тысяч часов после начала процесса нагружения.

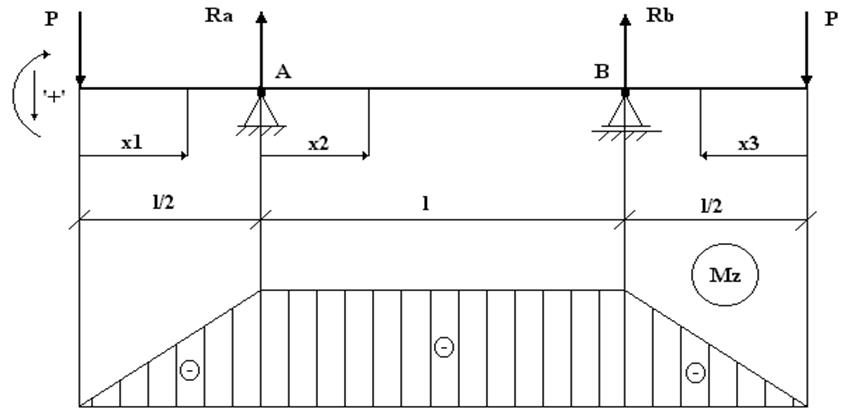
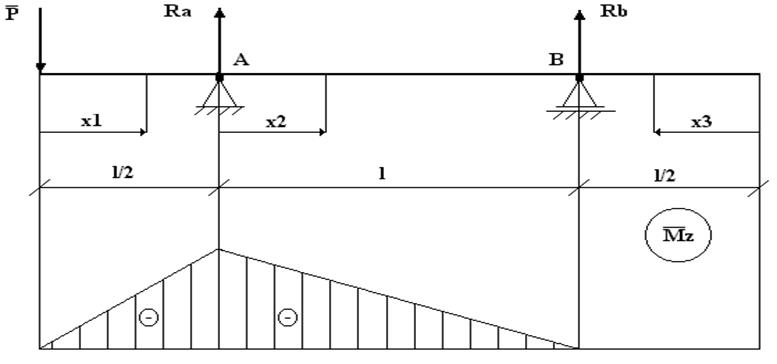
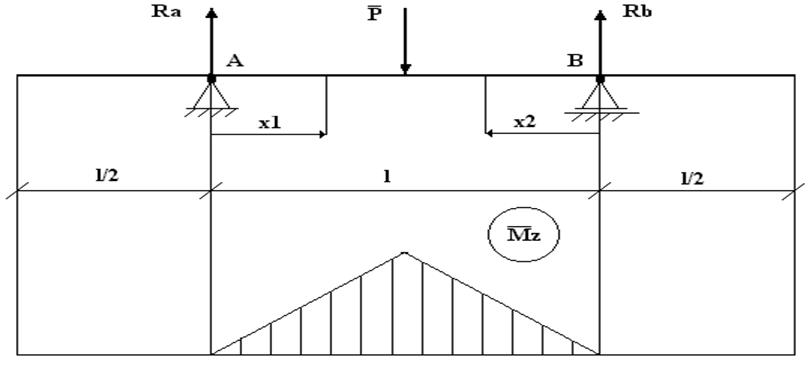
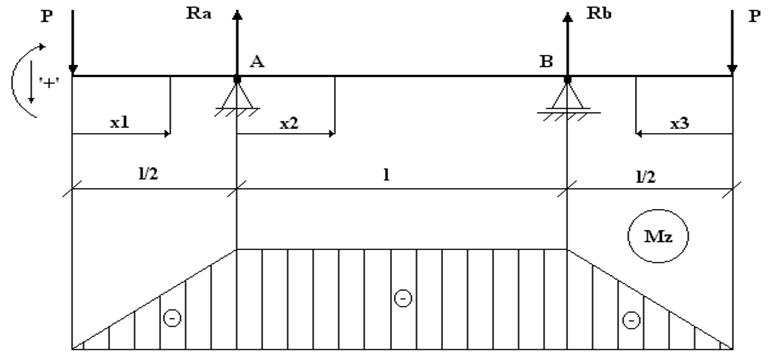
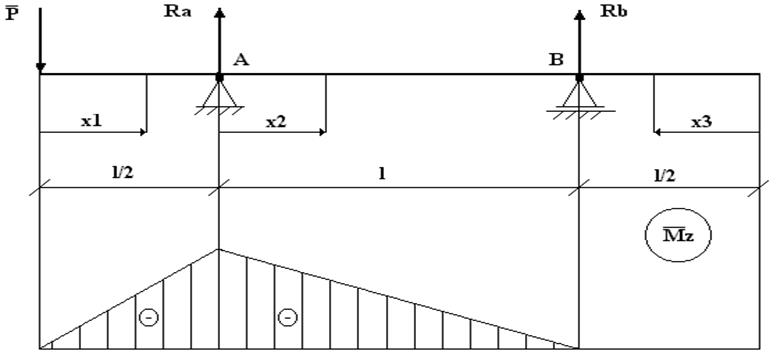
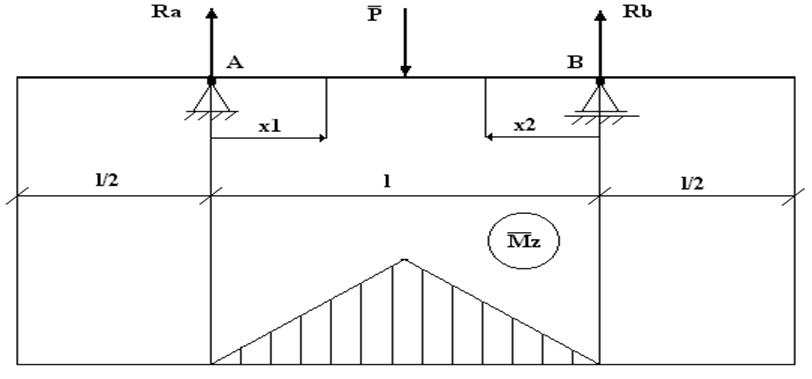
2. Расчетная схема

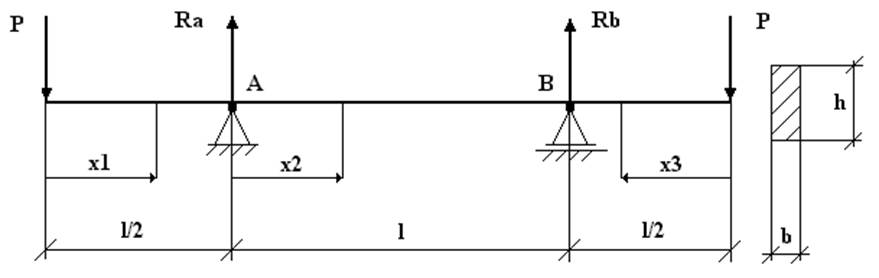
            3. Решение задачи

          3.1 Распределение нормальных напряжений по высоте балки

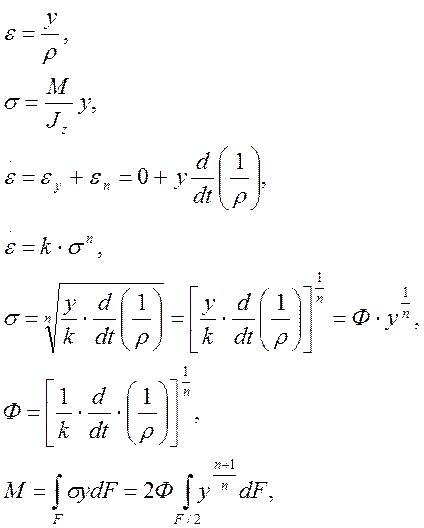
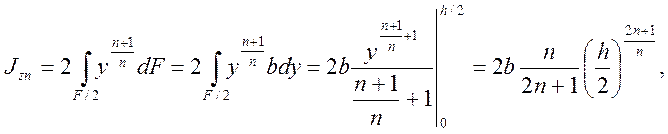
при n = 1:

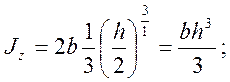
при n = 3:

Определим максимальный момент

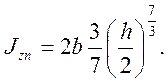
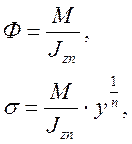
1)  участок №1

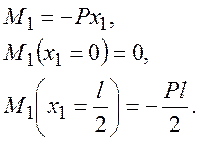
2)  участок №2

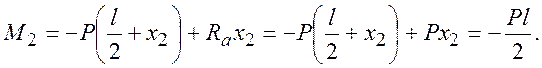
3)  участок №3

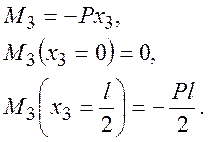
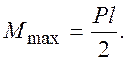
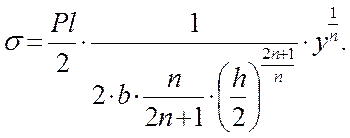
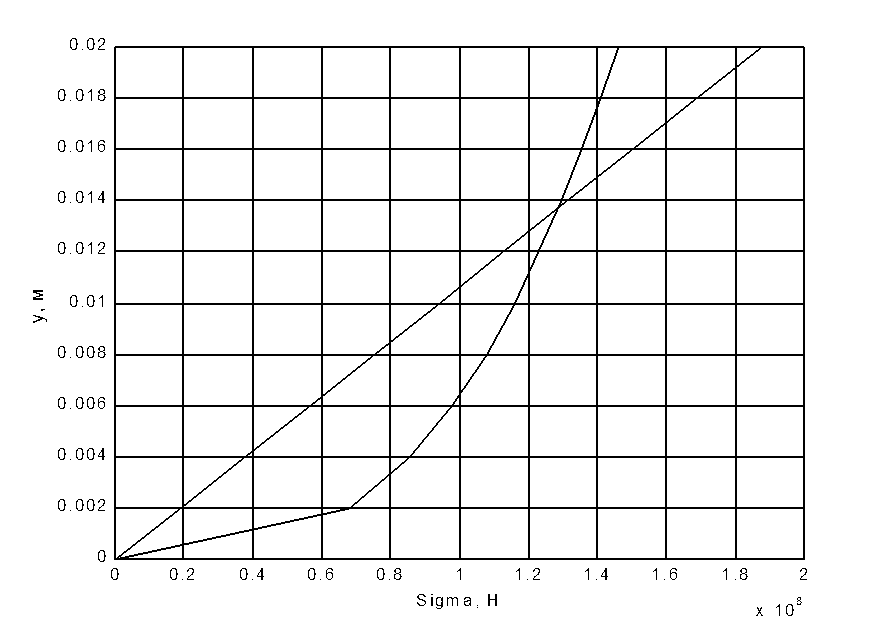
Результаты полученные машинной обработкой выведенной зависимости при n = 1 и n = 3

Y	Sigma 1 (n=1), МПа	Sigma 2 (n=3), МПа
0	0	0
0,0020	18,75	67,69
0,0040	37,50	85,28
0,0060	56,25	97,63
0,0080	75,00	107,45
0,0100	93,75	115,75
0,0120	112,50	123,00
0,0140	131,25	129,49
0,0160	150,00	135,38
0,0180	168,75	140,80
0,0200	187,50	145,83

            Распределение нормальных напряжений по высоте сечения при n = 1 и n = 3 

Определим прогибы при статической нагрузке методом Мора:

1) участок №1

           

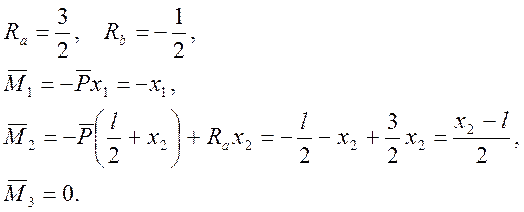
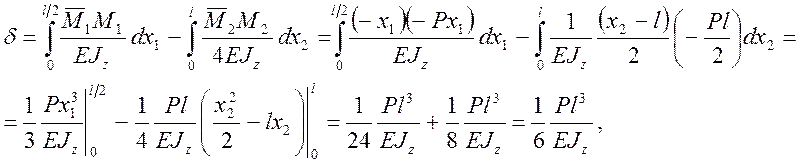
δ = 0,49 см.

2) участок №2

           

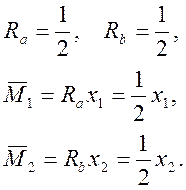
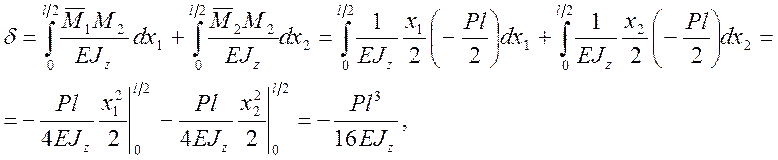
δ =  -0,18 см.

3.3 Максимальный прогиб через десять тысяч часов после начала процесса    

нагружения

           

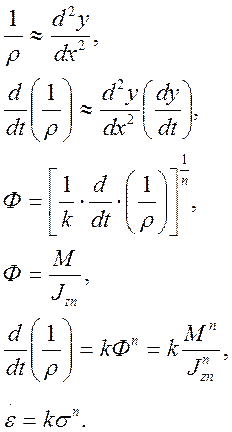
1) участок №1

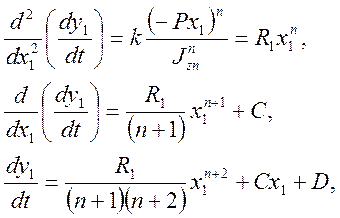
2) участок №2

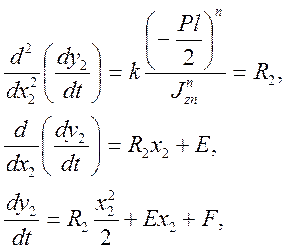
            Граничные условия:

                                                       

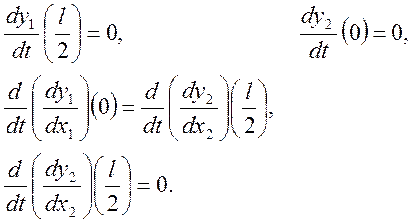
Составляем систему уравнений:

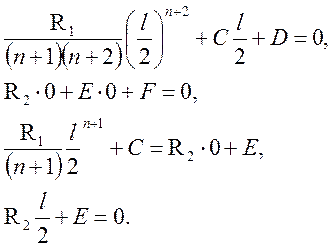
Решение системы уравнений:

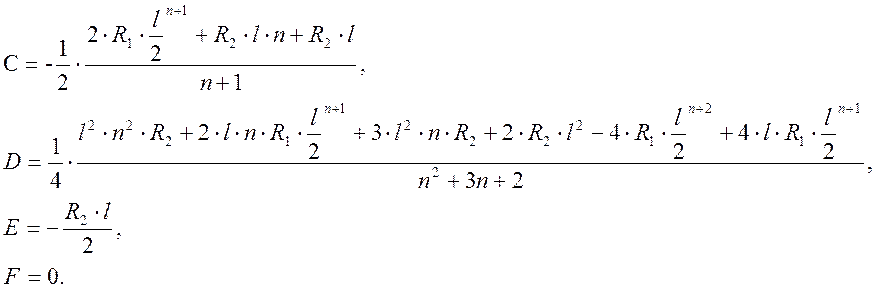
            Подставляем значения постоянных интегрирования в систему:

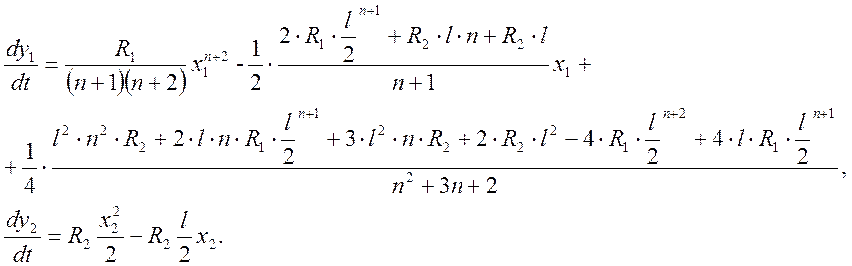
            Подставляем вместо  и  соответственно 0 и  (на участке №1 прогиб в нуле, а на   

участке №2 посередине стержня),  получаем:

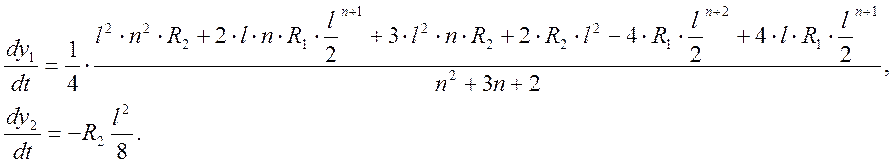
            Интегрируем по времени, постоянные интегрирования при этом являются прогибами

            при статической нагрузке на первом и втором  участках соответственно :

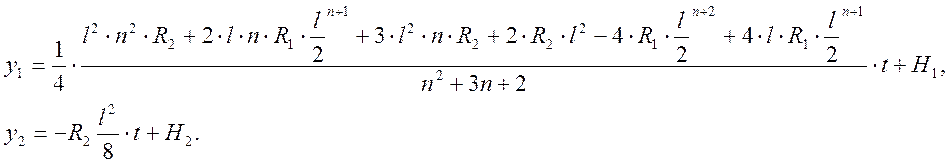
            Решая систему уравнения с учетом подстановки исходных данных получаем:

           

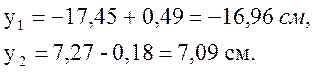
            Промежуточный итог:

           

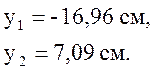
            Вывод по краю стержня прогиб является максимальным:

           

1. Формулировка задания для двутавра №12

Балка двутаврового сечения h = 120 мм, b = 64 мм, d = 4,8 мм, t = 7,3 мм, шарнирно закрепленная и нагруженная силами по концам величиной P = 4 кН. При температуре T = 500 °С. Материал – углеродистая сталь, коэффициент упругости Е = 1,6*10⁶ кГ/мм² , n = 3, k = 1,5 *10^-15 (см²/кГ)ⁿ *1/час.

Определить:

1) распределение нормальных напряжений по высоте балки, пренебрегая неустановившейся ползучестью;

2) наибольший прогиб через десять тысяч часов после начала процесса нагружения.

2. Расчетная схема

   

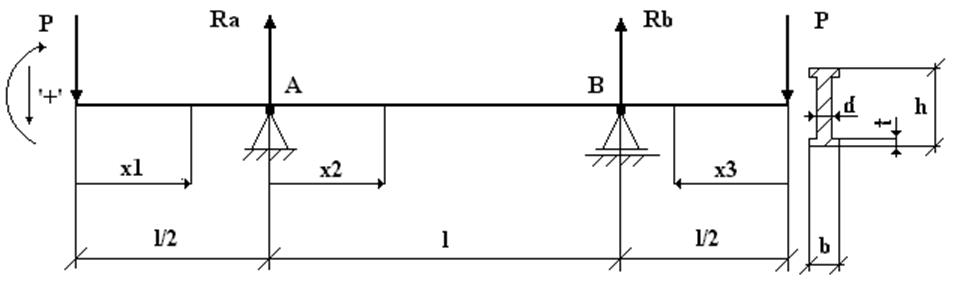
            3. Решение задачи

          3.1 Распределение нормальных напряжений по высоте балки

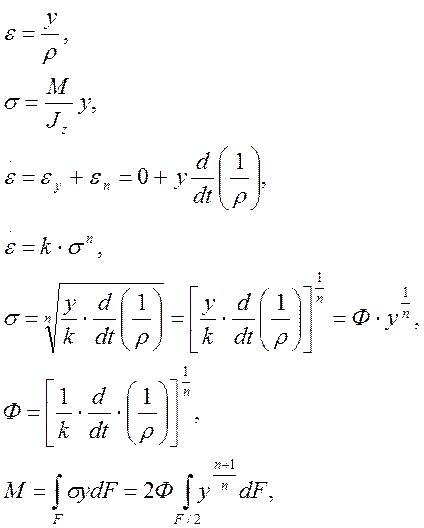
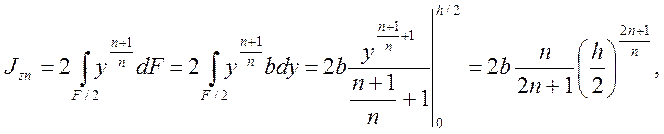
Момент инерции для данного сечения будет представлять собой сумму трех моментов инерции для прямоугольного сечения.

Момент инерции для первого прямоугольника

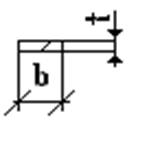
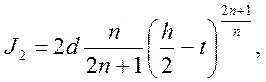
 Момент инерции для всего сечения:

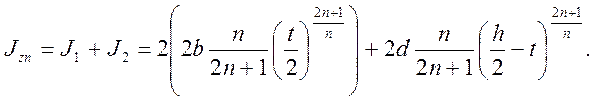
при n = 1:

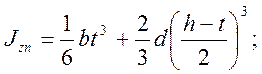
при n = 3:

Определим максимальный момент

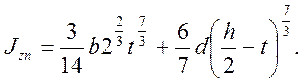
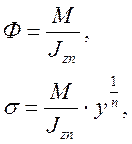
1) участок №1

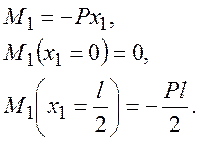
2) участок №2

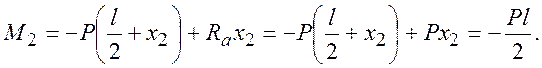
3) участок №3

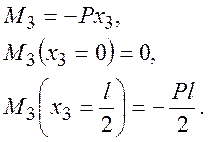
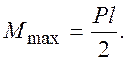
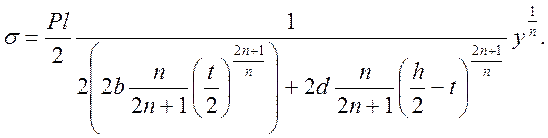
Результаты полученные машинной обработкой выведенной зависимости при n = 1 и n = 3

Y	Sigma 1 (n=1), МПа	Sigma 2 (n=3), МПа
0	0,00E+00	0,00E+00
0,005	1,06E+07	3,86E+07
0,01	2,12E+07	4,85E+07
0,015	3,17E+07	5,55E+07
0,02	4,23E+07	6,10E+07
0,025	5,29E+07	6,56E+07
0,03	6,35E+07	6,97E+07
0,035	7,41E+07	7,34E+07
0,04	8,47E+07	7,67E+07
0,045	9,52E+07	7,97E+07
0,05	1,06E+08	8,25E+07
0,055	1,16E+08	8,52E+07
0,06	1,27E+08	8,76E+07

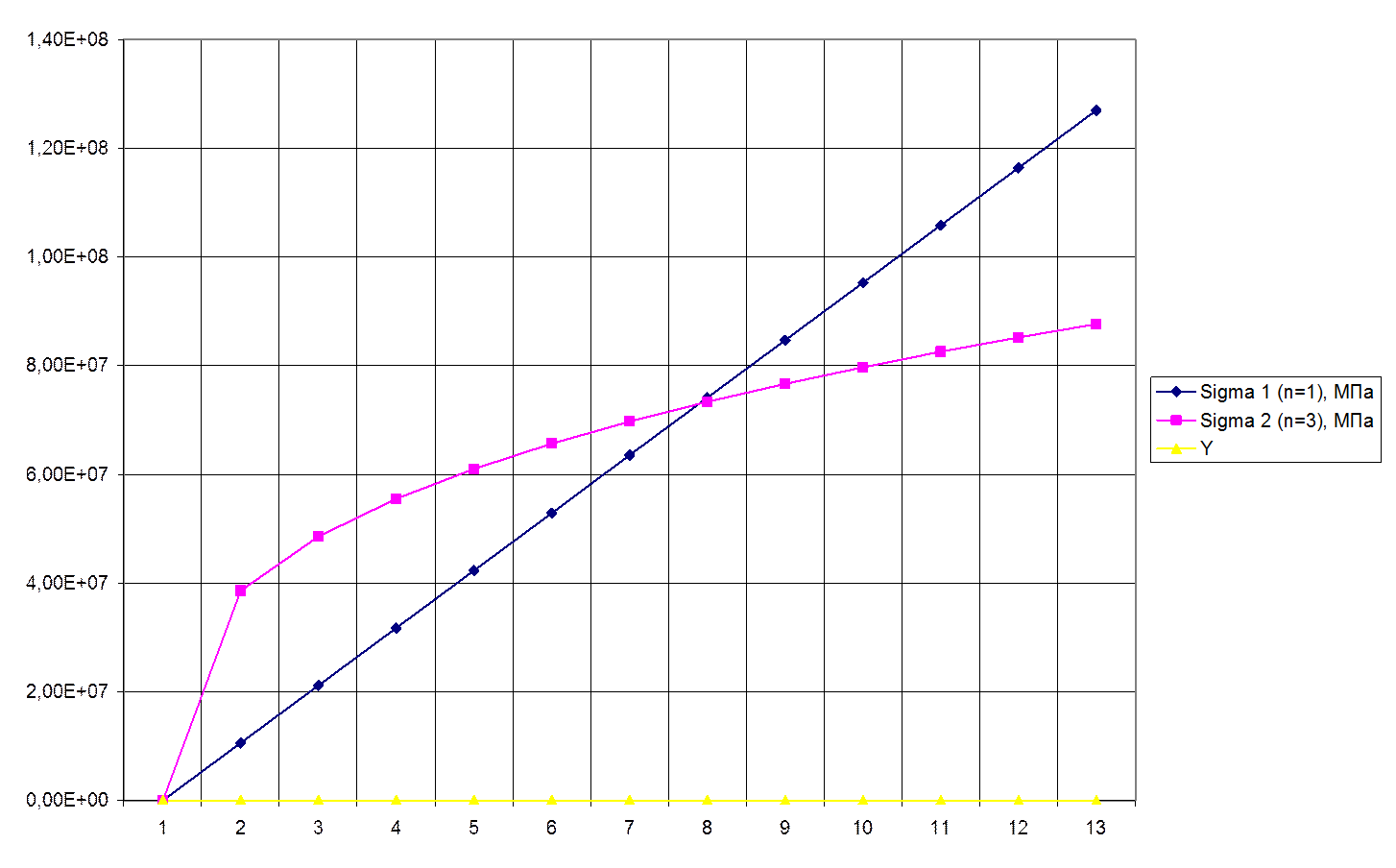
Определим прогибы при статической нагрузке методом Мора:

1) участок №1

           

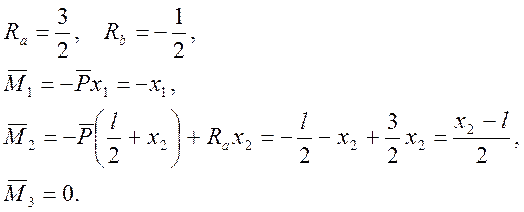
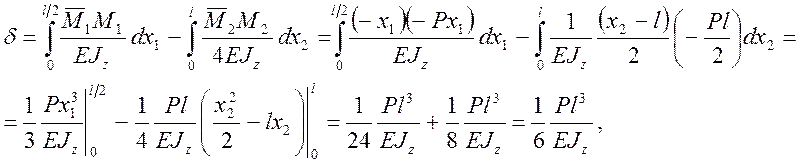
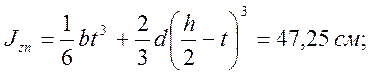
Прогиб статический на краю равен:

2) участок №2

           

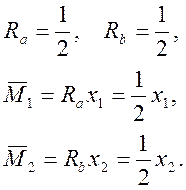
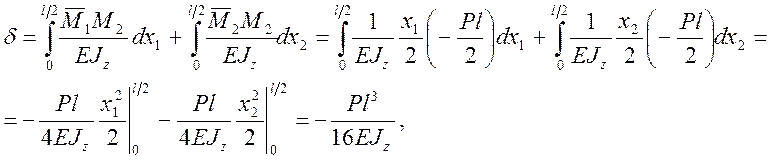
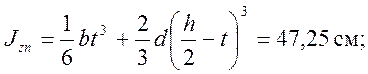
Прогиб статический посередине равен:

Решение системы уравнений аналогично решению в случае прямоугольного сечения.

Необходимо только посчитать прогибы с учетом изменившегося момента инерции.

С краю прогиб составляет

,

а посередине

Суммарный прогиб равен:

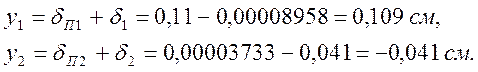
Вывод максимальный прогиб на краю стержня и равен 0,1 см.