Расчет элементов металлоконструкции на статическое и динамическое нагружение, страница 4

                                      z                                                                 X              

 Z                                                                  Рис.9

  Вычисление коэффициентов глобальной матрицы жесткости [K] производится по общим правилам МКЭ [3-6].

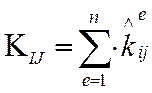 , где                                           (4.2.1.2)

  - коэффициент локальной матрицы жесткости прямолинейного элемента, произвольно ориентированного в глобальной (общей) системе координат (рис.9);

ij (IJ) - номера обобщенных перемещений в локальной (они же в глобальной) системе отсчета, одновременно принадлежащие хотя бы одному элементу; n- число КЭ, которые одновременно имеют оба (I и J) перемещения.

            Связь между локальной матрицей жесткости КЭ, произвольно ориентированного в глобальной системе отсчета XYZ, с матрицей жесткости того же элемента в локальной системе отсчета xyz [k^e], осуществляется через матрицу направляющих косинусов [L] в соответствии с зависимостью

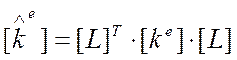                                             (4.2.1.3)

            Каждый коэффициент локальной матрицы жесткости k_ij^e представляет собой силу (или реакцию), возникающую в i – ом направлении при единичном смещении в j – ом направлении. Полная матрица жесткости является симметричной и содержит следующие, отличные от нуля, коэффициенты:

          k^e₁₁ = - k^e₁₇ = k^e₇₇ = - k^e₇₁ =EF/L ;

          k^e₂₂ = - k^e₂₈ = k^e₈₈ = - k^e₈₂ =12 EF_z /L³ ;

          k^e₂₆ = k^e_2.12 = k^e_6.2 = k^e_12.6 = - k^e_6.8 = - k^e_8.6 = - k^e_8.12 = k^e_12.8 = 6 EI _z / L₂;

          k^e_3.3 = k^e_9.9 = - k^e_3.9 = - k^e_9.3 = 12 EI _y / L³;

          k^e_3.3 = k^e_3.11 = - k^e_9.11 = - k^e_11.9 = k^e_11.3 = k^e_5.3 = - k^e_9.11 = - k^e_11.9 = 6 EI _y / L²;

          k^e_4.4 = - k^e_4.10 = - k^e_10.4 = k^e_10.10 =GI _x / L;

          k^e_5.5 = k^e_11.11 = 4EI _y / L;     k^e_6.6 = k^e_12.12 = 4 EI _z / L;

            k^e_5.11 = k^e_11.5 = 2EI _y / L;     k^e_6.12 = k^e_12.6 = 2 EI _z / L;

где      L – длина элемента;

E, G – соответственно, модуль упругости и сдвига;

F – площадь сечения;

I_x, I_y, I_z – моменты инерции поперечного сечения элемента относительно главных центральных осей.

Сформировав глобальную матрицу жесткости стержневой системы и зная вектор внешних сил {P}, обобщенные перемещения в глобальной системе отсчета определяются решением системы линейных уравнений (4.2.1.1).

Затем, выбирая из столбца {D} только те, которые относятся к одному

КЭ {D}®{}, осуществляется переход к локальным перемещениям базового элемента (рис.10).

{D^e} = [L]^T {}.

                                                 y,Y

 

                                     _{5       2                                                        8}

                                                                                              ₁₁

                          _{1                                                                                     7}   x,X

                             _{6                                                                            10}

                                             _{4                                                       12}

                            z,Z      _{3                                               9}

                                                               Рис.10

По найденным перемещениям {D^e} и известной матрице жесткости элемента [k^e] определяются внутренние усилия, действующие в концевых сечениях элемента:

{P^е} = [k^е] {}.

Нумерация и положительное направление этих усилий соответствуют обозначениям рис.10

Дальнейший расчет напряжений, возникающих в каждом элементе cистемы, осуществляется по правилам расчета на сложное сопротивление.

4.2.2. Исходные данные программы stud03

     5    1

    69   23

          DY