Для формирования матриц в выражении (8.1.6) все
необходимые параметры определяются из начальных условий или известны. В
результате решения (8.1.6) определяются обобщенные перемещения в конце
временного шага {![]() }. По
соотношениям (8.1.3) и (8.1.5) определяются соответствующие обобщенные скорости
и ускорения для рассматриваемого момента времени. При кажущейся простоте,
описанная методика расчета динамики систем с большим числом степеней свободы
имеет довольно сложный алгоритм и ориентирована на использование мощных ЭВМ.
}. По
соотношениям (8.1.3) и (8.1.5) определяются соответствующие обобщенные скорости
и ускорения для рассматриваемого момента времени. При кажущейся простоте,
описанная методика расчета динамики систем с большим числом степеней свободы
имеет довольно сложный алгоритм и ориентирована на использование мощных ЭВМ.
В тех случаях, когда реакция системы определяется на заданное кинематическое возмущение (вектор внешних сил может быть равен нулю), целесообразно решение уравнения (8.1.5) осуществлять с учетом корректировки на каждом временном шаге граничных условий по перемещениям.
Процедура учета сложных граничных условий заключается в следующем:
1. Зависимость известных перемещений от времени (например, перемещений точек крепления системы) представляется некой функцией (гармоникой, рядом Фурье или задается табличным способом при известном заранее шаге счета по времени).
2.
В матрице [![]() ] отыскивается
строка, в которой диагональный элемент К
] отыскивается
строка, в которой диагональный элемент К![]() соответствует
заданному перемещению
соответствует
заданному перемещению ![]() (t). В
этой строке все коэффициенты, за исключением К
(t). В
этой строке все коэффициенты, за исключением К![]() ,
обнуляются. Соответствующая компонента Р
,
обнуляются. Соответствующая компонента Р![]() из
вектора {
из
вектора {![]() } заменяется
произведением К
} заменяется
произведением К![]()
![]() (t).
(t).
3.
Все остальные строки матрицы [![]() ]
преобразуются путем переноса известного произведения К
]
преобразуются путем переноса известного произведения К![]() (t) ( (i = 1,2,…n);
i
(t) ( (i = 1,2,…n);
i![]() ) в правую часть.
) в правую часть.
4.
Массивы [![]() ] и {
] и {![]() } преобразуются столько раз, сколько
задано перемещений.
} преобразуются столько раз, сколько
задано перемещений.
Расчет конструкции на сейсмичность осуществляется программой dinam2d.
8.2. Результаты расчета программы.
Результаты расчета программы приведены для трех точек. В них найдены перемещения в трех взаимоперпендикулярных плоскостях (по трем степеням свободы ). Также найдена скорость в одной из точек.
Рис.21
Рис.22 Перемещения в 1 точке по 79,80,81 степеням свободы
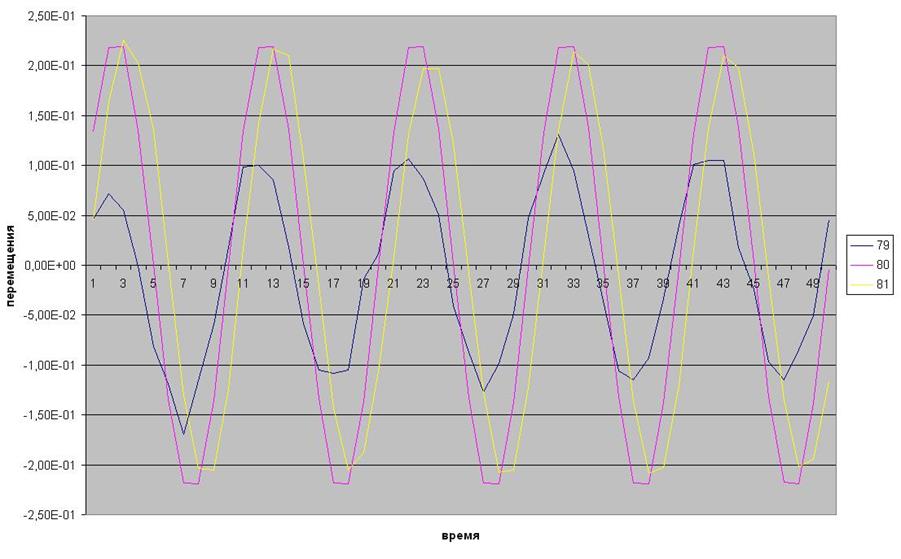
Рис.23 Перемещения во 2 точке по 1, 2, 3 степеням свободы
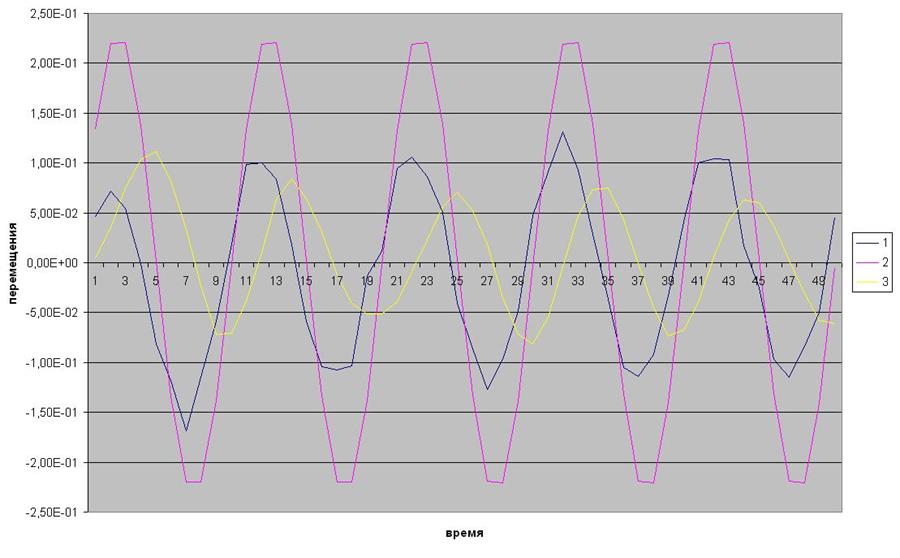
Рис.24 Перемещения в 3 точке по 1171, 1172, 1173 степеням свободы
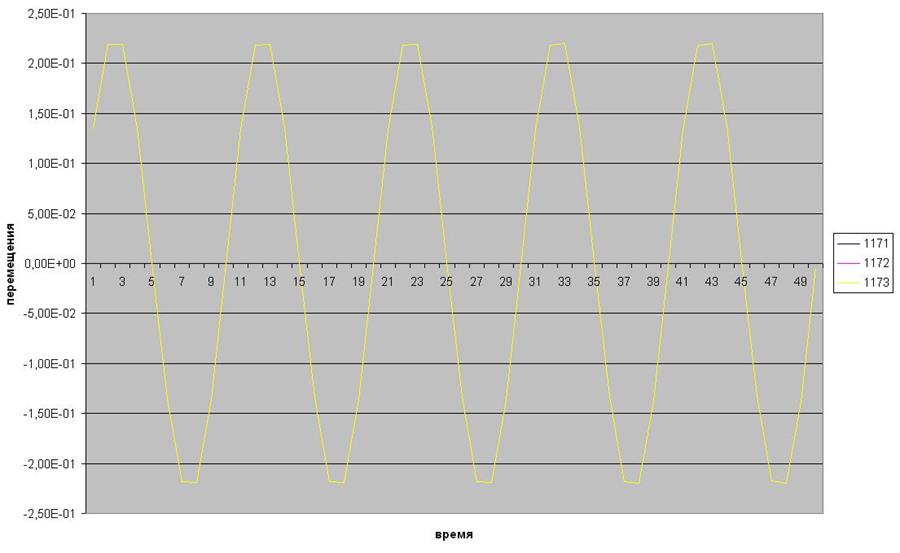
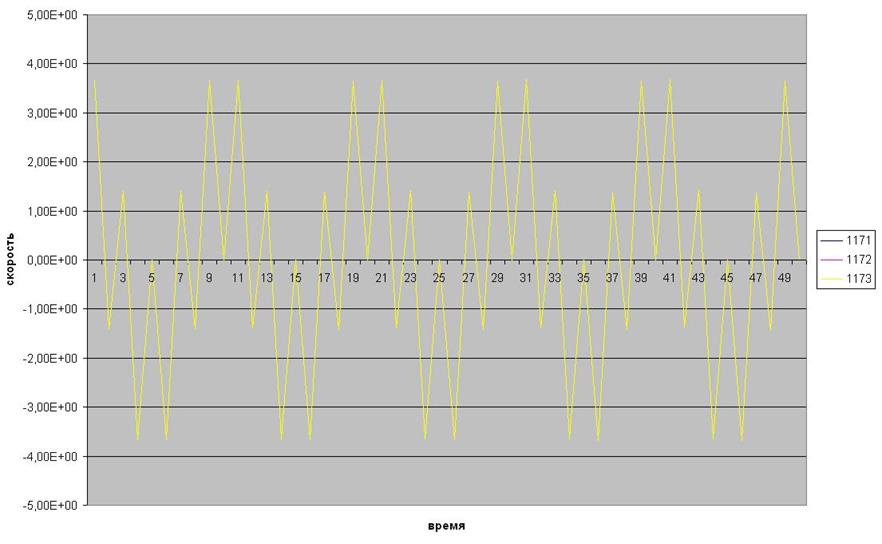
Рис.25 Скорость в 3 точке по 1171, 1172, 1173 степеням свободы
Заключение:
В данной работе произведен расчет элементов металлоконструкции на различные воздействия. В результате можно с уверенностью сказать, что использование составных конструкций вместо цельных (составной колонны вместо цельной, ферменной конструкции вместо цельных балок из стандартных профилей) значительно (в 1.5 – 2 раза) экономят строительный материал.
В работе осуществлен подбор сечений элементов металлоконструкции при заданных условиях о не превышении допускаемых напряжений.
Также в работе был произведен расчет собственных частот и форм колебаний металлоконструкции. В результате получены значения собственных частот в Гц: .1355E+01 .1915E+01 .1961E+01 .2093E+01 .2344E+01
Найденные формы колебаний приведены в работе.
Произведенный расчет на сейсмичность показал, что в заданных условиях(сейсмичность – 7баллов) конструкция «работает» без перегрузок.
Список использованной литературы:
1. Расчетные и курсовые работы по сопротивлению материалов / Ф.З. Алмаметов, С.И. Арсеньев, Н.А. Курицын, А.М. Мишин – М.: Высш. шк., 2003. – 367с
2. СНиП 2.01.07 -85. Нагрузки и воздействия.
3. Сопротивление материалов /В.И. Феодосьев- М.: МГТУ им. Н.Э.Баумана, 2003 -592с.
4. Метод конечных элементов в технике/ Зенкевич О. - М.:Мир, 1975 - 410с.
5. Алгебраическая проблема собственных значений./ Уилкинсон Дж. Х. М.: Наука, 1970 -564с
6. Численные методы решения динамических задач механики деформируемого твердого тела./ Арсеньев С.И., Титух И.Н. - С. Петербург, БГТУ, 1997 - 72с.
7. Расчеты машиностроительных конструкций методом конечных элементов. Справочник./ Мяченков В.И., Мальцев В.П., Майборода В.П. - М: Машиностроение, 1989.-520с
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.