Расчет элементов металлоконструкции на статическое и динамическое нагружение, страница 3

4. Расчет цельной балки и составной конструкции на прочность.

В качестве несущей балки, как и в случае с опорными балками, могут выступать как цельная балка так и составная(ферменная) конструкция.

Ниже будут произведены расчеты цельной балки и составной конструкции. Будут найдены параметры сечения цельной балки и составной конструкции, при условии выдерживания одной и той же нагрузки, и ограничения максимального прогиба балок.

4.1. Расчет на прочность несущей балки с исполненной из стандартных профилей.

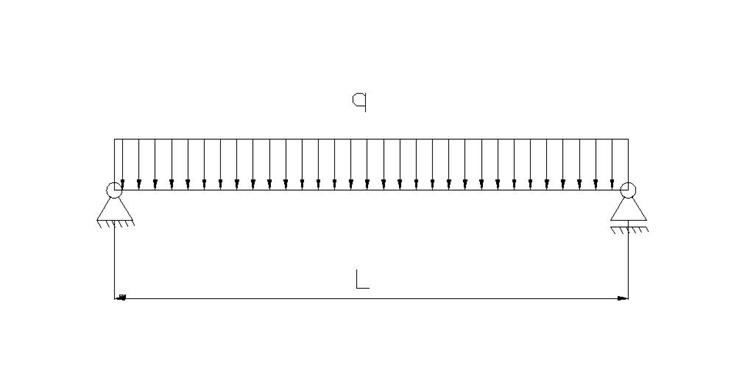Рис.6

Длина балки L=15м; Допускаемый прогиб балки [d]=7,5см

Действующая на балку распределенная нагрузка определяется исходя из снеговой нагрузки на горизонтальную проекцию покрытия. Значение веса снегового покрова на один квадратный метр следует принимать в зависимости от снегового района по данным табл.4 [2]. Для заданного 3 снегового района вес снегового покрова =100кг/см²

Тогда распределенная нагрузка действующая на балку равна:

q=b*(50+S*K_НАД)=1710 кг/м

Максимальный момент возникает в середине балки(при L/2) и равен:

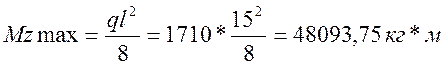
Момент сопротивления равен:

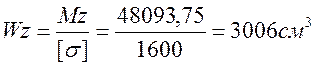
Из таблицы 3 приложения 6 [1] по моменту сопротивления  выбираем два двутавра №50 стоящих друг на друге.

Wz=2*1589=3178см³

Момент инерции для двух двутавров стоящих друг на друге равен:

Jz=(Jz₁+r²*F₁)*2=(39727+25²*100)*2=204454 см⁴

Максимальный прогиб балки определяется энергетическим методом (вычислением интеграла Мора)

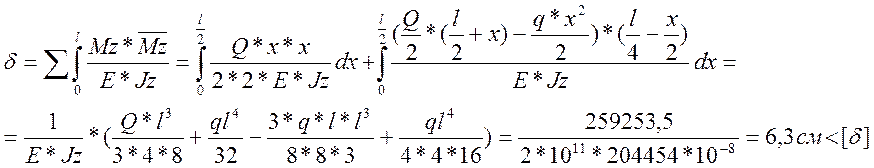
Максимальный прогиб меньше допускаемого, следовательно выбранное сечение удовлетворяет всем условиям.

Масса всей балки равна :

m_балки=15*2*78,5=2355 кг

4.2. Расчет несущей балки исполненной с виде ферменной конструкции.

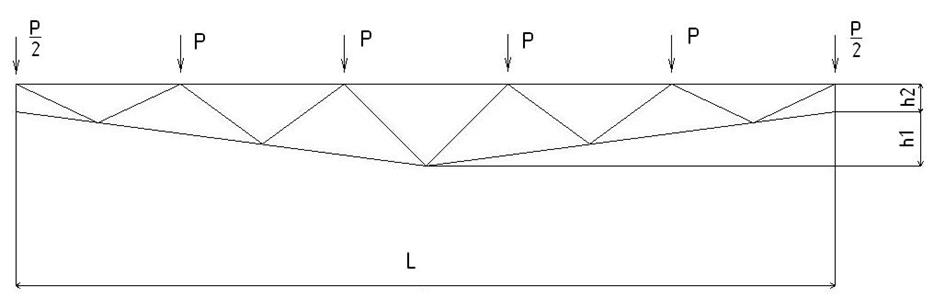Рис.7

P = 5130 кГ

L = 15м

h1 = 1м

h2 = 0,5м

Поперечные сечения балок

                 Рис.8

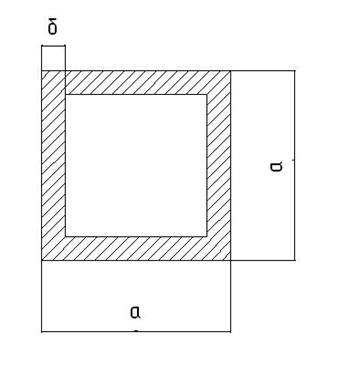
   Наружных балок                                 Внутренних балок

   a1 = 16 см                                             a2 = 5 см

   d1 = 0,8 см                                           d2 = 0,2 см

   Jz1=Jy1= 1878 см⁴                               Jz2=Jy2= 14,77 см⁴

   Jk1 = 2809 см⁴                          Jk2=22,12 см⁴

   S1 = 48,64 см²                          S2=3,84 см²

Расчет фермы на статическую нагрузку производится программой stud03

4.2.1. Статический расчет.

            В основу статического расчета (под действием собственного веса или сосредоточенных сил), положен матричный метод, являющийся частным случаем метода конечных элементов (МКЭ), так как функции формы являются аналитически точными (функции Эрмита), вследствие чего результат решения основного уравнения

                                                   (4.2.1.1)

получается также, в рамках гипотез сопротивления материалов, аналитически точным. В выражении (4.2.1.1):

            [K] – глобальная матрица жесткой системы;

            {D} – разрешенные обобщенные перемещения (линейные и угловые);

            {P} – столбец обобщенных внешних сил.

                Y                                                     _{8   11}     x                                    

                                                                                             ₇                             

                                                              ₁₂                      10                        

                                                                       ₉                                             

               y       _{5       2}                                                                                      

                                                ₁

                                                                                                                    

                   _{6    3          4}