q = w*hmin/3=332,8*5/3=554,67 Н/м
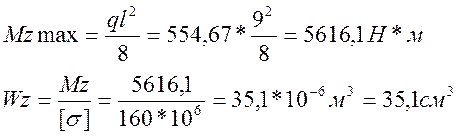
Из таблицы 3 приложения 6 [1] выбираем швеллер № 12
7. Расчет собственных частот и форм колебаний конструкции.
Определение собственных частот и форм колебаний конечно-элементной модели конструкции производится решением нестандартной задачи на собственные значения [4].
![]() w
w![]() =0 ,где
(7.1)
=0 ,где
(7.1)
[K] - глобальная матрица жесткости;
[M]=[M]![]() + [M]
+ [M]![]() ,
,
[M]![]() - диагональная матрица масс системы,
учитывающая сосредоточенные массы и их моменты инерции;
- диагональная матрица масс системы,
учитывающая сосредоточенные массы и их моменты инерции;
[M]![]() -матрица масс системы,
учитывающая распределенную (собственную) массу элементов;
-матрица масс системы,
учитывающая распределенную (собственную) массу элементов;
w![]() - спектр собственных
частот (i=1,2,…,n);
- спектр собственных
частот (i=1,2,…,n);
{U}![]() -
собственный вектор (нормированная форма колебаний системы на i-ой частоте);
-
собственный вектор (нормированная форма колебаний системы на i-ой частоте);
Формирование глобальной матрицы [M] осуществляется аналогично матрице [K]
в методе конечных элементов через коэффициенты локальной матрицы [M![]() ].
].
Представляя кинетическую энергию одного КЭ через квадратичную форму
Т = 0,5ë![]() û
û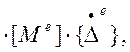
локальная матрица масс (инерции) будет иметь вид (приводится для плоского случая):
[Me] = m 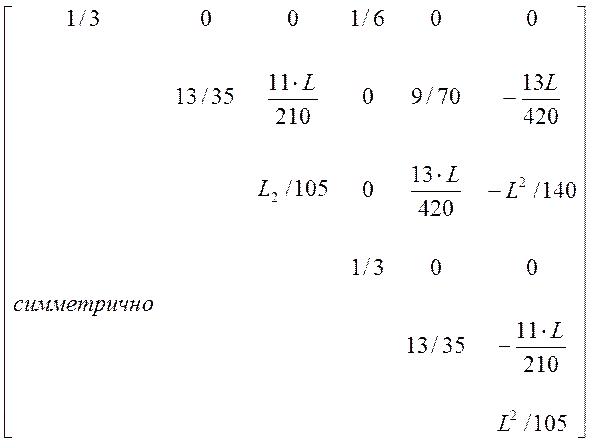
Собственные частоты и соответствующие им моды (формы) колебаний для систем с числом степеней свободы n > 500 целесообразно определять методом ортогонального спуска, который в отличии от метода обратных итераций [5] обладает лучшей сходимостью при определении низких, менее 1гц, собственных частот.
В конечномерной постановке задача формулируется как
[K] {u}i = li [M] {u}i , (7.2)
где li = wi2 - квадрат собственной частоты (i=1,2,...);
{u}i - собственный вектор (форма колебаний) для i-ой частоты.
Итерационный процесс необходимо строить с учетом
ортогональности собственных векторов, найденных на предшествующих итерациях ({u}![]() , {u}
, {u}![]() ,…, и т.д.), а именно
,…, и т.д.), а именно
![]() (7.3)
(7.3)
Задаваясь на первой итерации (n=1) произвольным вектором {X1}, определяется вектор {Z1} по соотношению (7.3). Затем решается система
[K] {y} = {Z} ,
в которой норма от найденных обобщенных перемещений ½½yn+1½½ равна l-1 при выполнении условия
½½yn+1½½ - ½½yn½½ < EPS.
Собственный вектор для найденной частоты по завершении итерационного процесса определяется как
{u}1={y1} / ½½y1½½.
Затем процесс повторяется, но уже с учетом {u}1 в (7.3).
При задании EPS=10-16, ошибка в определении первых пяти собственных частот не превышает (1…3)%.
Определение собственных частот и мод колебаний объекта «в лете», то есть не имеющего точек закрепления в пространстве, связано с рядом особенностей ввиду вырождения в этом случае описанных выше матриц жесткости и инерции.
Уравнение (7.2) преобразуется к виду:
[А] {u}i = li [M] {u}i , (1.7),
где [А] =[ К] -σ [M],
σ- сдвиг (некое произвольное положительное число).
Искомая собственная частота wi2 = li + σ. [3,9].
Для ускорения сходимости и локализации собственных значений в определенных пределах используется метод биссекции [6].
Нахождение собственных частот и форм колебаний конструкции осуществляется программой sobs03.
7.1. Результаты расчетов.
Рис.15 1 форма . f= 1,355 Гц
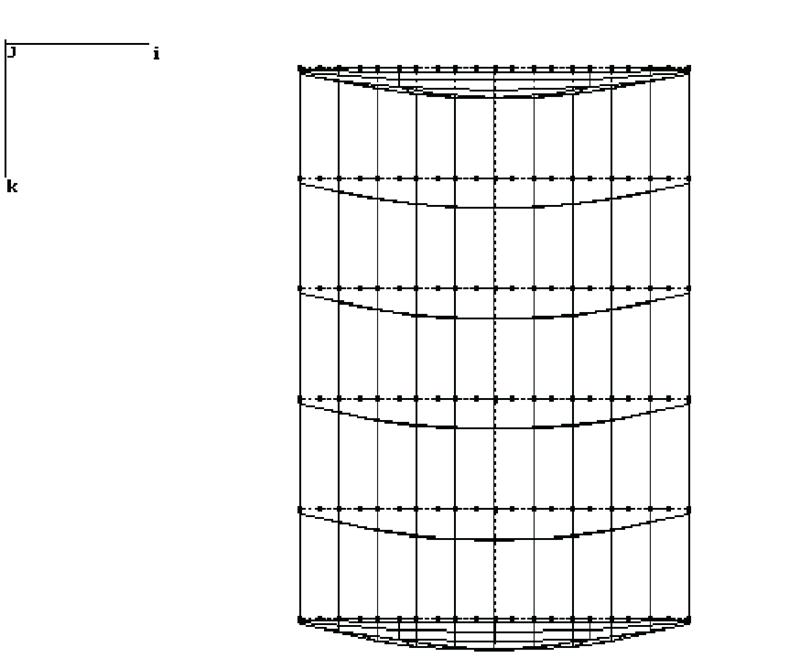
Рис.16 2 форма. f= 1,915 Гц
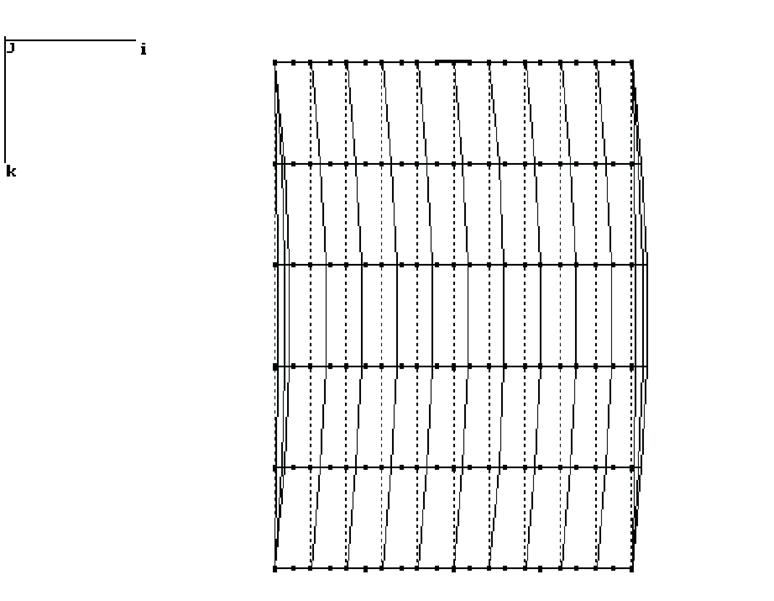
Рис.17 3 форма. f= 1,961 Гц
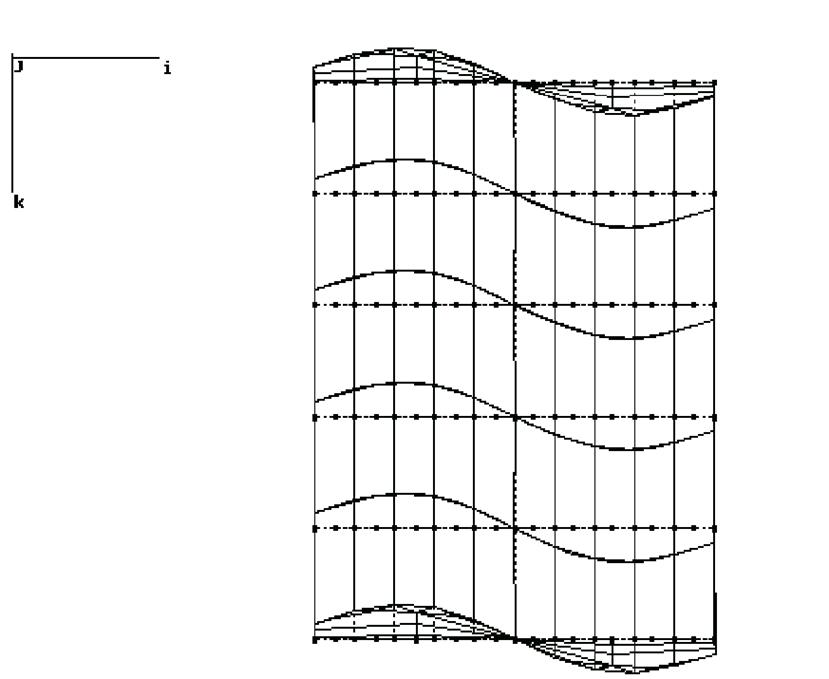
Рис.18 4 форма. f= 2,093 Гц
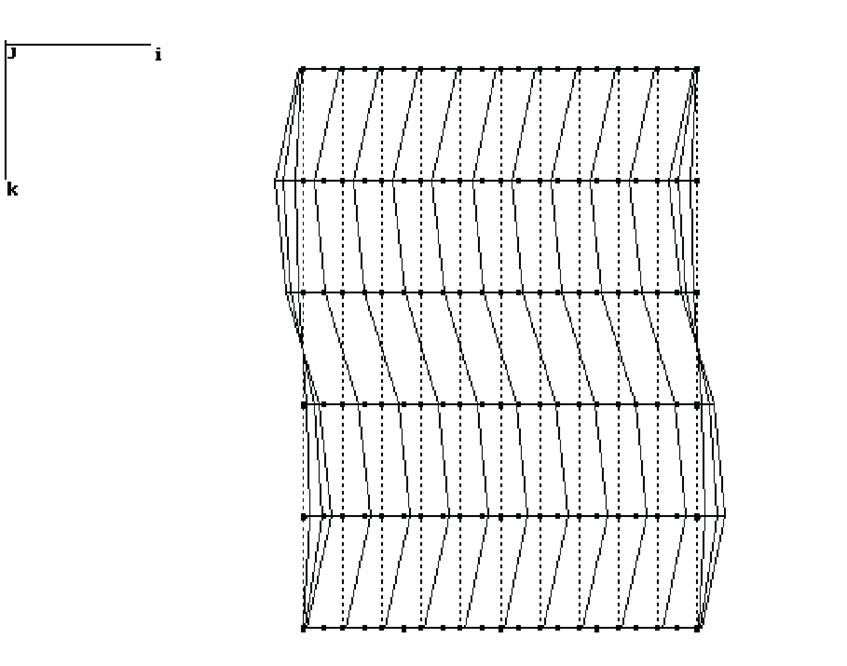
Рис.19 5 форма. f= 2,344 Гц
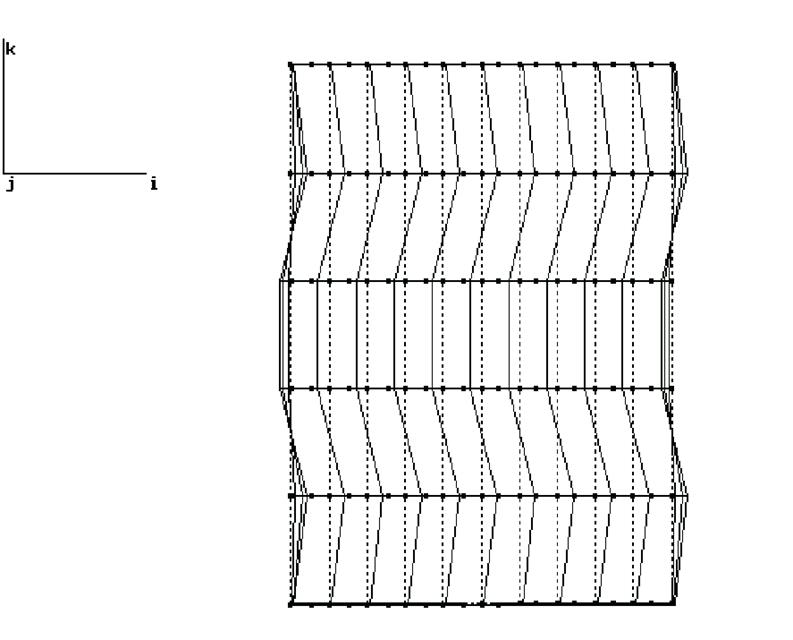
8. Расчет конструкции на сейсмическое воздействие.
Сейсмичность площадки - интенсивность возможных сейсмических воздействий.
Устанавливается в соответствии с картами сейсмического районирования, измеряется в
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.