Волновое уравнение. Конечноэлементная формулировка задачи. Метод суперпозиции гармоник

1. Волновое уравнение

     Во многих задачах течений невязкой жидкости приходится сталкиваться с основным уравнением вида

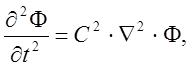                                                     (1)

где Ф — функция типа потенциала.

     Это уравнение обычно трехмерное и называется волновым. Оно относится к уравнениям гиперболического типа, и для него необходимо задать как граничные, так и начальные условия.

1.1.  Конечноэлементная формулировка задачи

       К волновому уравнению может быть применен метод конечных элементов. Вариационную формулировку для двухмерной задачи, соответствующую уравнению (1), можно записать в следующем виде:

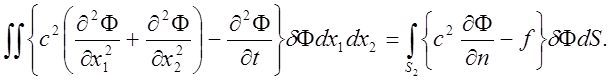               (2)

Предполагается, что на поверхности S₁ выполняется условие и .  После интегрирования выражения (2) по частям  получим

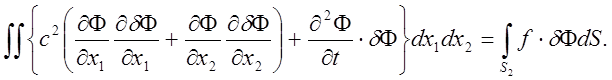              (3)

    Потенциал Ф можно аппроксимировать в пределах каждого элемента как

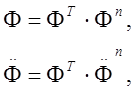                                           (4)

где F-интерполяционная функция; Fⁿ и -узловые неизвестные.

     Подставив выражения (4) в уравнение (3),  получим для одного элемента

                                         (5)

где

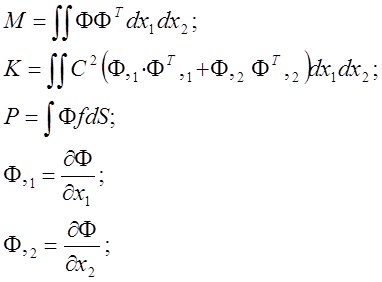
     После  объединения всех элементов имеем следующее матричное уравнение для всей области:                    

                             (6)

Уравнение (6) легко решается в случае гармонического движения, когда возмущение и ответная реакция  на него находятся в фазе, т. е. когда                        j

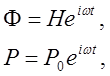                                            (7)

где i=;  w—круговая частота.                        .

      Такой случай характеризует динамически установившийся режим и соответствует моменту, когда после начала возмущения прошло достаточно времени.

Подставляя выражения (7) в уравнение (6), получаем

                                          (8)

Если частота w известна, то можно решить систему уравнений (8) для заданной величины P₀ . В частности, если P₀ = 0,  урав­нение (8) сводится к нахождению собственных значений (w_i) и собственных векторов (Н_i) , которые дают решение системы.

         Важно указать, что для задач, связанных с исследованием гармонического установившегося состояния, точность конечноэлементного  решения в значительной степени зависит от размеров сетки, конечных элементов. Эта зависимость выражается как функция от параметра r:

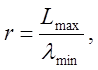
где L_max — максимальный размер наибольшего элемента; l_min- минимальная длина волны.

         Эта величина, определяющая максимальный характерный размер элемента, должна быть, как правило, не более 0,1. Упомянутый метод решения применим для установившихся задач. Если Р есть произвольная функция времени Р(t) , то можно решать задачу методом суперпозиции или прямого интегрирования. Ниже обсудим технику решения с помощью первого метода.

1.2.Метод  суперпозиции гармоник.

       Рассмотрим уравнение (6) которое запишем в виде

                            (9)

Как и ранее, предположим, что используется минимум главных краевых условий. Следовательно, матрица К , равно как  матрица М, является положительно определенной. Заметим, что если определенные элементы матрицы Ф известны и отличны от нуля (обозначимих ), то после умножения на соответствующий

столбец К они дадут в правой части уравнения вектор . Допустим ,что ускорения на границе области, соответствующие этим значениям Ф, равны нулю. Следовательно, выражение (8) можно  записать в виде

                                      (10)

где К, М и Р — новыематрицы, приведенные к удобномувиду.

  В методе суперпозиции гармоник сначала рассматривается  случай свободных колебаний, т. е. уравнение (8). Это дает последовательность собственных чисел и собственных векторов,  которые можно записать как

w_i, F_i  для   i=1, 2, . . . , n ,

где все w_i — положительны для положительно определенных матриц К и М.                                                                                                                                        Согласно определению

                                         (11)

ВекторыF_i ортогональны матрицам К и М, т. е.

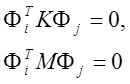        для i¹j,                            (12)

и эти произведения не равны нулю, когда i = j. Каждый собственный вектор содержит произвольную постоянную, которая обычно находится из условия нормированияF_i относительно М:

                                           (13)

Это приводит к соотношению

                                                (14)

   Решение для вектора Ф можно записать как комбинацию S различных собственных векторов и вектора с известными значениями :

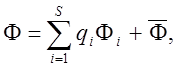                           (15)

где s£ n и  q_i =q_i(t) можно рассматривать как обобщенные  координаты.

Подстановка Ф в уравнение (10) приводит к следующему равенству:

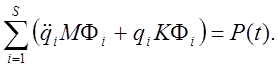                                (16)

Умножив предварительно это уравнение на  с учетом  условия ортогональности, получим s несвязанных между собой дифференциальных уравнений вида

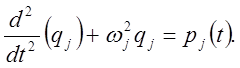                                   (17)

где

Решение уравнения (17) даст

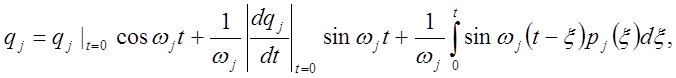            (18)

где x — переменная интегрирования.

Первые члены, равные нулю, если система находится первоначально в покое, содержат начальные условия. Суммируя вклады всех s форм, получаем

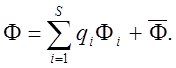                                   (19)

Основная трудность состоит в выборе s, т. е. в решении вопроса о том, сколько нужно взять обобщенных координат. Решение является точным, если s =n (термин «точное» относится в данном случае к решению дискретных уравнений).

1.3.Реакция прибрежных вод на гармонические возмущения.

          Рассмотрим специальный случай волнового уравнения, описывающего задачу определения реакции прибрежных вод на гармонические возмущения .Обозначения показаны на рис. 1. Пусть h(x₁ ,x₂ ,t) — возвышение свободной

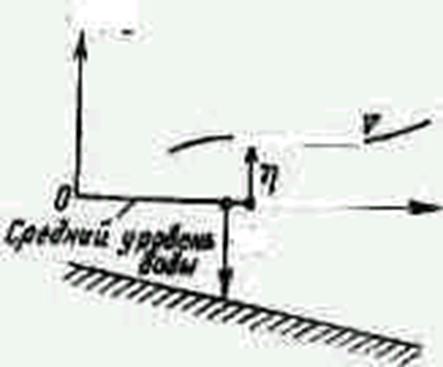
Рис.1. Гармоническое вынужденное движение.

Случай мелкой воды.

поверхности над уровнем моря. Будем оперировать с  проинтегрированными вертикальному направлению  величинами q₁ и q₂ ,  которые в этом случае являются функциями от x₁ , x₂ и t:

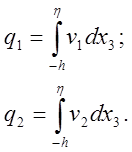                              (20)

Допустим также, что амплитуда h мала по сравнению с первоначальной глубиной h , и пренебрежем силой Кориолиса и горизонтальным трением. Будем считать, что давление равно гидростатическому давлению:

P=gr(h-x₃).                                        (21)