Математика \ Основы метода конечных элементов

Волновое уравнение. Конечноэлементная формулировка задачи. Метод суперпозиции гармоник, страница 2

Это уравнение заменяет третье уравнение движения, а два остальных будут иметь вид

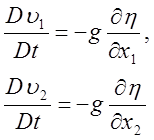                                      (22)

Запишем уравнение неразрывности:

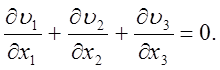                                  (23)

Применим кинематическое граничное условие, согласно которому вертикальная скорость при  x3 = h равна изменению высоты  волны во времени (рис. 1) , т. е.

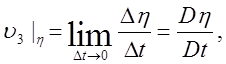                                     (23)

где

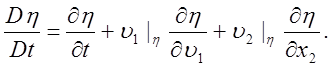                                  (25)

Проинтегрировав уравнение неразрывности по x3c  использо­ванием правила Лейбница, т. е.

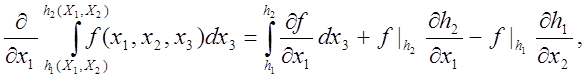
и подставив выражение (25) в уравнение (23) , получим

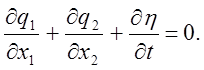                           (26)

Далее проинтегрируем по x3 уравнения количества движения. Используя правило Лейбница и кинематическое граничное условие на свободной поверхности, находим                 

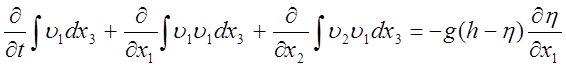                 (27)

и аналогичное уравнение в направлении  x2.

Пренебрегаяконвективными членами в уравненияхколичествадвижения иучитывая, что амплитуда h мала посравнению с h, запишем

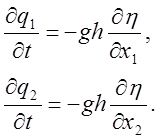                                   (28)

На береговой границе зададим проинтегрированную (по вер­тикали) нормальную скорость: qn = an1q1+an2q2= на S2. На границе с открытым морем определено отклонение от среднего уровня  h=h’(x1,x2,t)  на S1. Дифференциальные уравнения

(26) и (28)  можно преобразовать к одному уравнению второго порядка. Для этого необходимо продифференцировать выражения (28) соответственно по x1 и x2 и подставить их в уравнение неразрывности (26), в свою очередь продифференцированное предварительно по t. В результате получим

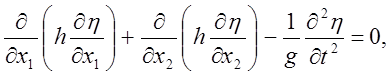                                 (29)

где       h=h’ на S1;

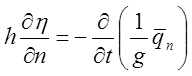    на S2.                                    (30)

Граничное условие для нормальной скорости заменено уравнением равенства сил в направлении нормали, что согласуете с увеличением порядка основного дифференциального уравнения задачи.                                                 

Резонанс и вынужденные колебания, вызванные гармоническим возмущением свободной поверхности , можно исследовать,  представить h как

h(x1,x2,t)=H(x1,x2)ei wt,                                        (31)

где w — круговая частота.

Тогда выражение (29) приводится к следующему виду:

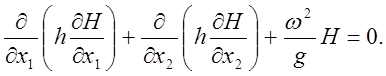                                  (32)

Для возмущения свободной поверхности

H=H’   на   S1;

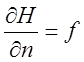                                        на   S2.                                 (33)

Для случая свободных колебаний зададим ряд однородных граничных условий

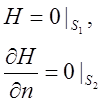                                   (34)

и определим частоты и формы колебаний.

В случае гармонического движения уравнения (32) принимают вид

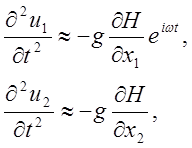                                  (35)

где u1 и u2 — горизонтальные перемещения.

Уравнения (35) после интегрирования в пределах полупериода дают для максимальных горизонтальных смещений

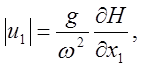                               (36)

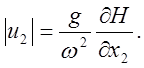                               (37)

1.4.1.Формулировка задачи в рамках метода конечных элементов.

 Из уравнения (32)  и граничных условий можно записать следующее выражение применительно к методу взвешенных невязок:

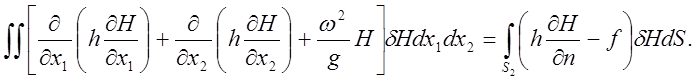                             (38)

Интегрируя его по частям, находим

 

Скачать файл