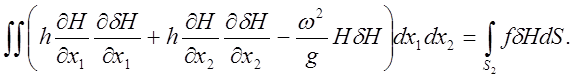Волновое уравнение. Конечноэлементная формулировка задачи. Метод суперпозиции гармоник, страница 3

                                                                         (39)

Если f = 0, правая часть уравнения (39) равна нулю.

Предположим, что в пределах элемента переменная Н может быть аппроксимирована выражением.

                               (40)

где F — интерполяционная функция; Нⁿ — узловые неизвестные .

 Тогда для элемента

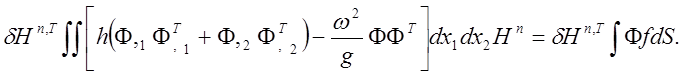                      (41)

 Выражение (41) можно записать как

                                              (42)

где

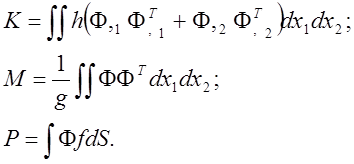
Матрицы К, М, Р аналогичны матрицам, входящий в выражение (41). Для всей области имеем

KH-w²MH=P,                                                     (43)

Где К и М-симметричные матрицы.

 

Пример.  Если известны частота волн и уровеньсвободной поверхности на границе рассматриваемого района с открытии морем, уравнение (43)  можно записать в следующем виде

                                                          (К-w²М)Н=Р’,

 где элементы вектора Р’ получаются как результат перемножения известных возвышений свободной поверхности Н’ на элементы матриц К и w²М и перенесения произведения в правую часть. Решив представленное уравнение , можно получить величины возвышения свободной поверхности в виде ряда.

        В качестве иллюстрации рассмотрен Данканский бассейн, построенный во второй мировой войны в гавани залива Тэйбл в Южной Африке.

Этот бассейн тщательно исследовался в связи с характерной особенностью

залива, в котором он расположен, заключающейся в значительном уселение приливных волн определенных частот. Факт усиления клебаний

установлен модельным экспериментом, гармоническим анализом записей волн и простым теоретическим решением, которое может в данном случае дать приемлемые  результаты, так как форма бассейна близка к прямоугольной.

      Экспериментальные значения амплитуд волн в месте расположении причалов Е и О изображены на рис.2 в приложении. Заметим, что первый значительный период составляет примерно Т= 11,45мин(теоретически значение) и ясно  прослеживается в экспериментальной кривой, хотя колебания на ней сильно демпфированы. Это демпфирование можно было ожидать, посколько период Т=11,45мин (теоретически) соответствует свободному » и вытеканию воды из бассейна, чего в  действительности не наблюдалось.

   Решение методом конечных элементов  выполнено путем  деление бассейна на168 треугольных элементов с шестью узлами в каждом, что дало 377 узловых неизвестных (вторичная сетка.). Значения периодов составляли Т=1,2,3, . . . мин (w= 2p/Т — круговая частота), а значения возвыше­ния свободной поверхности во всех узлах на входе в бассейн Н’=1. Положение свободной поверхности в местах расположения причалов Е и О показаны на рис.1.

Найдены собственные числа системы. При этом в целях уменьшения машинного времени использовалась первичная сетка. Эти значения сравнивались со значениями ,полученными из решения уравнения  для Т=1,2,3,. . .мин. Результаты сравнения показали хорошие согласования. 

Литература

1. Сегерлинд , Ларри Дж  “Применение метода конечных элементов” М: “Мир”, 1997г.

2. Бреббиа и Конор  “Метод конечных элементов для решения задач жесткости”