Интегралы Вали (расчетные задания), страница 6

Ответ:  

Задача 19.15.

Условие: Вычислить длину дуги кривой, заданной уравнениями в полярных координатах.      ρ = 5(1 – cos φ),     0 ≤ φ ≤ .

Решение: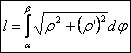                              

ρ´ = 5(1 – cos φ)´ = 5 sin φ;        (ρ´)² = 25 sin² φ;            ρ² = 25(1 – cos φ)².

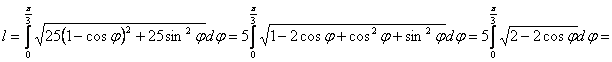
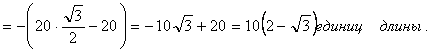
Ответ:  

Задача 20.15.

Условие: Вычислить объем тела, ограниченного поверхностями.

Решение:                                - эллипсоид.

Плоскости перпендикулярны оси Oz.

;

;

;    ;

;                   .

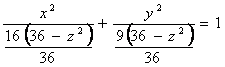S(z) = π·ab – площадь поперечного сечения;       .

;

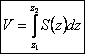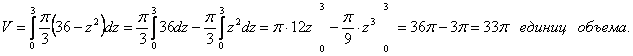
Ответ:   .

Задача 21.15.

Условие: Вычислить объем тела, образованного вращением фигуры, ограниченной графиками функций. Ось вращения .

Решение:Найдём точки пересечения графиков:

;

x⁶ = x;

x (x⁵ – 1) = 0;

x₁ = 0,   x₂ = 1.

.

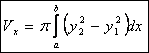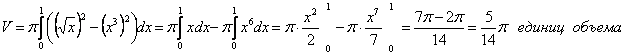
Ответ:  

Задача 22.15.

Условие: Определить работу (в джоулях), совершаемую при подъеме спутника с поверхности Земли на высоту  км. Масса спутника равна  т, радиус Земли  км. Ускорение свободного падения  у поверхности Земли положить равным 10 м/с².

Решение:m = 5т = 5·10³ кг;  H = 400 км = 4·10³ м;  R_З = 6380 км = 6, 38·10⁶ м.

drFтяж                                     Hr = H + RЗ                                    RЗ

A = Fтяж · S · cos 180. ,          где     γ = 6, 67·10-11 ;                    МЗ = 6·1024 кг.