Интегралы Вали (расчетные задания), страница 5

x₁ = 6;           x₁ = 3π – 6;          x₂ = 6;        x₂ = 9π + 6.

x´(t) = 6(t – sin t)´ = 6(1 – cos t)

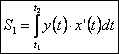
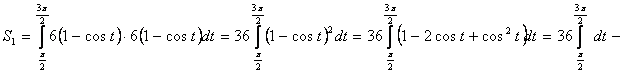
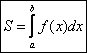
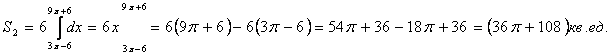
S = S₁ – S₂ = (54π + 144 - 36π – 108) кв.ед. = (18π + 36) кв.ед.

Ответ:   (18π + 36) кв.ед.

Задача 16.15.

Условие: Вычислить площадь фигуры, ограниченной линиями, заданными в полярных координатах.

Решение: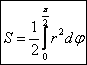

 

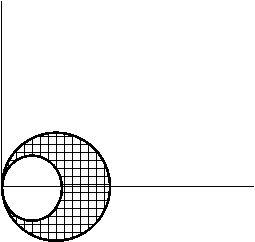0                                                    o

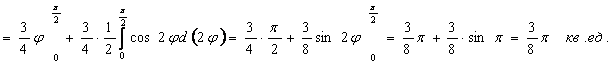
Ответ:  

Задача 17.15.

Условие: Вычислить длину дуги кривой, заданной уравнениями в прямоугольной системе координат.

Решение: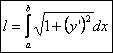

y´ = - e^x;           (y´)² = e^2x;

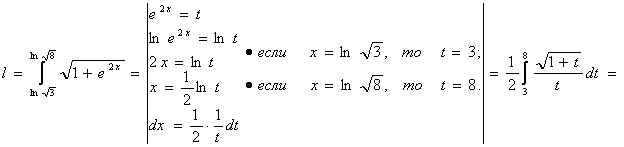
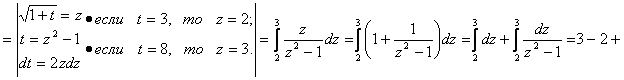
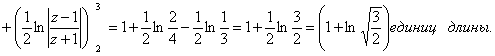
Ответ: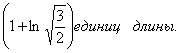  

Задача 18.15.

Условие: Вычислить длину дуги кривой, заданной параметрическими уравнениями.

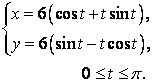
Решение: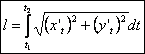                              

x´_t = 6(cos t + t sin t)´ = 6(- sin t + sin t + t cos t) = 6t cos t.

(x´_t)² = 36t² cos²t.

y´_t=6(sin t - t cos t)´=6(cos t – (cos t + t · (- sin t)))=6(cos t - cos t + t sin t)=6t sin t.

(y´_t)² = 36t² sin²t.