Интегралы Вали (расчетные задания), страница 4

Решение:Данный интеграл, вида

a = b = 1 – действительные числа;

m = - 2, n = , p =  - рациональные числа.

=> данный интеграл является интегралом от дифференциального бинома.

Ÿ  p =  - дробное;

Ÿ   - дробное;

Ÿ   - целое.

=> подстановка , где S – знаменатель дроби p.

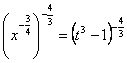;  ;  ;   - замена;  =>  ;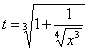

;           .

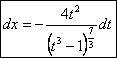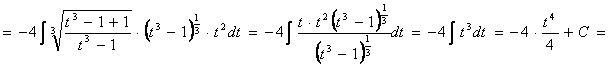
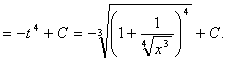
Ответ: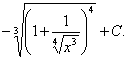  

Задача 14.15.

Условие: Вычислить площадь фигуры, ограниченной графиками функций.

y = arctgx,                    y = 0,                   x = .

Решение: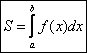                                    

x                                         x =                                                        0 y = 0                                                x      y = arctgx         -

Ответ: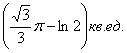  

Задача 15.15.

Условие: Вычислить площадь фигуры, ограниченной линиями, заданными уравнениями.

Решение:

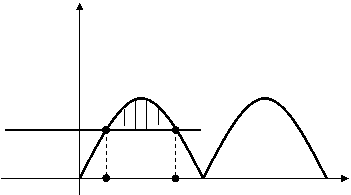             y

≤ t ≤ y = 6             0   3π-6     9π+6   12π

;       cos t = 0;       t = ; t1 = ;            t2 = ;    x