Условие прочности 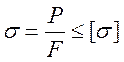 справедливо
для стержней с параметрами поперечного сечения, соразмеримыми с длиной
(например, куб).
справедливо
для стержней с параметрами поперечного сечения, соразмеримыми с длиной
(например, куб).
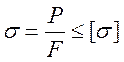
 , где
, где 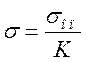
K – коэффициент запаса прочности
![]() для пластичных материалов, K = 1,5
для пластичных материалов, K = 1,5
![]() предел прочности для хрупких
материалов, K = 2 ÷ 3
предел прочности для хрупких
материалов, K = 2 ÷ 3
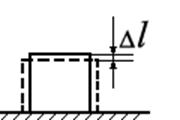
Если размеры поперечного сечения стержня значительно меньше его длины, то такой называют гибким.
Если гибкий стержень нагрузить сжимающей силой, то он может потерять устойчивость.
Устойчивость – это способность тела сохранять первоначальную форму равновесия.
Типы равновесия для гибких стержней подобны типам равновесия в теоретической механике, а именно равновесие абсолютно твёрдого тела может быть устойчивым, безразличным и неустойчивым.
|
|
|
|
|
устойчивое равновесие |
безразличное равновесие |
неустойчивое равновесие |
|
|
|
|
Критической нагрузкой называется нагрузка, при которой сжатый стержень теряет способность сохранять прямолинейную форму равновесия.
Потеря устойчивости гибких стержней происходит при напряжениях значительно больших допускаемых.
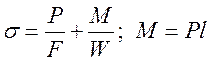
Основная задача в расчётах на устойчивость – это определение критических нагрузок.
Вывод формулы Эйлера для критической силы.
Рассмотрим сжатый стержень в критическом состоянии, который перешёл от прямолинейной формы к изогнутой
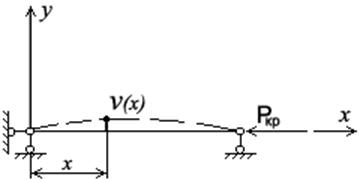
Приближённое дифференциальное уравнение изогнутой оси балки имеет вид:
![]()
![]() Знак минус, так как прогиб
положителен в данном случае, а момент отрицателен (выпуклость вверх)
Знак минус, так как прогиб
положителен в данном случае, а момент отрицателен (выпуклость вверх)
![]() .
.
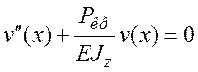 . Обозначим
. Обозначим 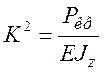
![]() . Линейное уравнение второго
порядка. Общее решение, известное из математики имеет вид:
. Линейное уравнение второго
порядка. Общее решение, известное из математики имеет вид:
![]() , где A и B – коэффициенты
интегрирования, определяются из граничных условий.
, где A и B – коэффициенты
интегрирования, определяются из граничных условий.
1. ![]() . Получим
. Получим ![]()
Тогда
![]() .
.
2. ![]() .
. ![]()
![]() , т.к. если
, т.к. если ![]() , то
стержень прогибов не имеет, что противоречит условию задачи.
, то
стержень прогибов не имеет, что противоречит условию задачи.
Тогда: ![]() . Это может быть при
. Это может быть при
![]() , где
, где ![]() - любое целое число.
- любое целое число.
![]() не даёт решения.
не даёт решения.
Тогда: ![]()
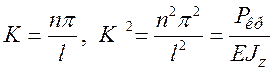
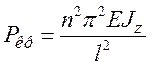 - формула Эйлера для критической нагрузки
потери устойчивости сжатого стержня при шарнирном закреплении его концов.
- формула Эйлера для критической нагрузки
потери устойчивости сжатого стержня при шарнирном закреплении его концов.
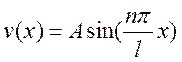 - уравнение прогибов стержня при потере
устойчивости.
- уравнение прогибов стержня при потере
устойчивости.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.