Определение главных центральных моментов инерции заданного сложного составного поперечного сечения и построение эллипса инерции

Определить главные центральные моменты инерции заданного сложного составного

 поперечного сечения и построить эллипс инерции.

Для решения поставленной задачи необходимо определить:

1)  координаты центра тяжести сечения;

2)  положение главных осей инерции;

3)  значение главных моментов инерции;

4)  провести проверку правильности определения значений главных моментов инерции, и положения главных осей инерции;

5)  определить значения радиусов эллипса инерции;

6)  построить эллипс инерции;

7)  исследовать, как изменятся главные моменты инерции, если последовательно изменить одно или два простых сечения.

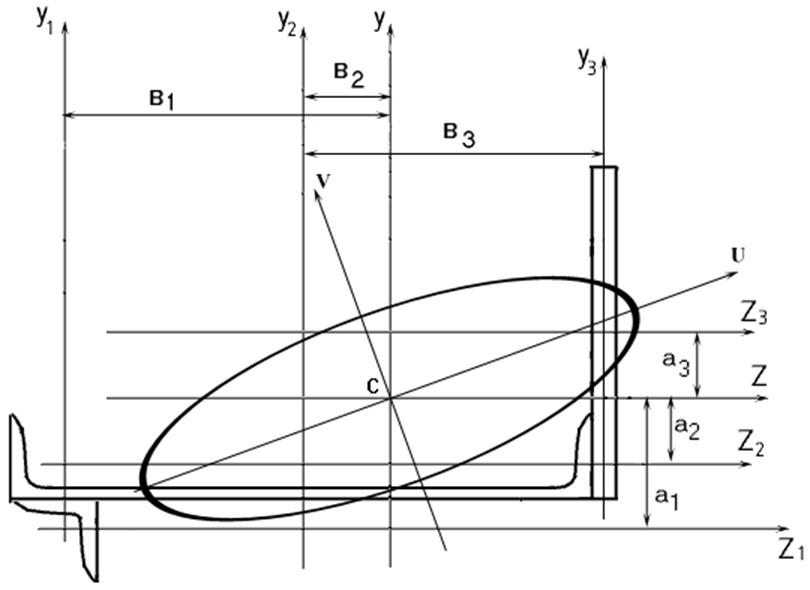
Выполнить расчет для схемы приведенной на рис.1. Сложное сечение состоит из равнобокого уголка с параметрами 60х60х8, швеллера № 22а, прямоугольника 180х20 (см), каждому из которых присваивается свой номер: 1 – уголок, 2 – швеллер, 3 – прямоугольник.

Рис.1. Общая и частные системы координат

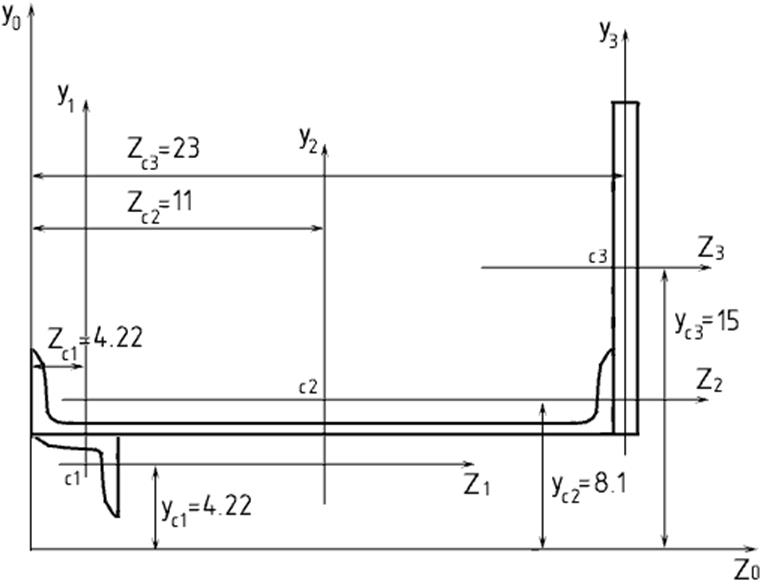
1.  Координаты центра тяжести всего сечения определяются:

,

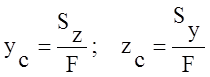где с – центр тяжести сечения;

F – площадь всего сечения – ;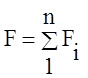

S_z, S_y – статические моменты – .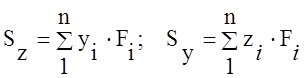

Выбирается произвольная система координатных осей У₀Z₀, в которой определяется согласно чертежу положение центров тяжести каждого простого сечения (, ). Рекомендуется оси произвольной системы координат проводить через крайние нижнюю и левую точки сечения.

Для прокатных профилей (рис.2. и рис.3.) выписываются из таблиц площадь сечений, моменты инерции относительно собственных центральных осей, центробежные моменты инерции. Для прямоугольных сечений (рис.4.) эти параметры рассчитываются по формулам.

Рис.2. Равнобокий уголок

В приведенном примере U1, V1 – главные оси уголка.

Для равнобоких уголков необходимо вычислить центробежный момент относительно центральных осей У₁Z₁:

.

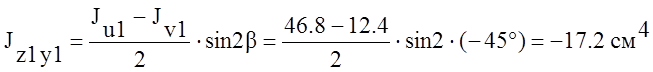Угол b отсчитывается от оси U₁ до оси Z₁. В случае движения по часовой стрелке угол b считается отрицательным.

В нашем случае b = – 45°.

Для неравнобоких уголков угол b выбирается из таблиц.

Рис.3. Швеллер

 

Рис. 4. Прямоугольное сечение

Все исходные данные рекомендуется привести в форме таблицы, с которой удобно будет работать за ЭВМ.

Номер элемента	1 – уголок	2 – швеллер	3 – прямоугольник
Площадь F	9.03	31.84	36.00
Координата	4.22	11.00	23.00
Координата	4.22	8.10	15.00
Момент инерции J	29.60	157.80	972.00
Момент инерции J	29.60	2393.90	12.00
Момент инерции	-17.20	0.00	0.00

Вычисления выполняются по программе «Определение главных центральных моментов и построение  эллипса инерции».

2.  Значения центральных моментов инерции всего сечения вычисляются:

; ;

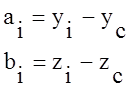
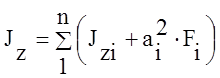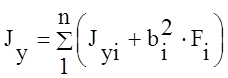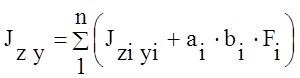
3.  Значения главных моментов инерции, угол наклона главных осей составного сечения.

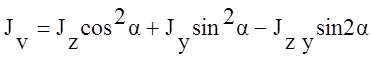
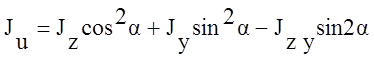
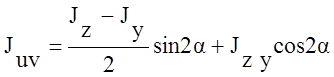
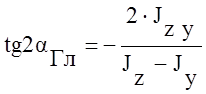
4.  Значения радиусов эллипса инерции

; 

Порядок работы с программой

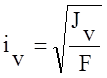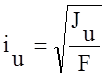
1.  В соответствии с запросом на экране дисплея ввести количество элементов N в сечении.

2.  Отвечая на запросы  программы,  ввести  параметры  F, z, y, R_z, R_y, R_zy  элементов  сечения.

3.  По окончании набора параметров каждого элемента на экран выводятся введенные значения, что позволяет произвести их корректировку. Для этого, отвечая на вопрос о правильности исходных данных, необходимо ввести «0», если ошибки ввода данных отсутствуют, и ввести «1» в противном случае.
Если введена «1», то программа затребует повторного ввода параметров элемента.

4.  После ввода всех исходных данных на экран дисплея выводятся результаты расчета и вопрос: «Будете ли продолжать расчет? Если нет – введите 0, если – да введите 1». Если введен «0», то выполнение программы прекращается. Если введена «1», то необходимо продолжить диалог с программой.

5.  Отвечая на вопросы программы, ввести номер изменяемого элемента сечения и его новые параметры, после чего на экране появятся результаты расчета и запрос о продолжении расчета.

Оформление домашней расчетно-графической работы

          Результаты решения рассмотренного примера необходимо переписать в тетрадь в нижеприведенной форме.

Площадь сечения F	76,87
Координата центра тяжести сечения Z c	15,82
Координата центра тяжести сечения Уc	10,88
Расстояния между осями a1, а2, а3	-6,66; -2,78; 4,12
Расстояния между осями в1, в2, в3	-11,60; -4,82; 7,18
Центральный момент инерции сечения Jz	2417,08
Центральный момент инерции сечения Jy	6246,18
Центробежный момент инерции Jzy	2172,00
Угол наклона главной оси инерции a (в градусах)	24,30573
Главный момент инерции сечения Ju	1436,27
Главный момент инерции сечения Jv	7226,98
Сумма центральных моментов инерции	8663,25
Сумма главных моментов инерции	8663,25
Центробежный момент инерции относительно главных осей Juv	0,00
Радиус инерции сечения iu	4,32
Радиус инерции сечения iv	9,70
Главные моменты инерции при замене швеллера № 10 Ju , Jv	2483; 449
Главные моменты инерции при замене уголка № 10 Ju , Jv	3441; 674

Равенство сумм центральных и главных моментов  инерции  свидетельствует о правильности выполнения расчетов. Проверкой решения является также равенство нулю центробежного момента инерции в главных осях. (R_uv) = 0.

При оформлении пояснительной записки студент должен привести условие задачи, все данные для отдельных простых сечений, сводную таблицу исходных данных, результаты решения и окончательный чертеж составного сечения, построенного в масштабе с обозначением всех осей и построенным эллипсом инерции.

Эллипс инерции для наглядности разрешается строить в произвольном масштабе.

Если J_zy > 0, то главная ось с наибольшим моментом инерции проходит через    квадраты     II и IV , если  J_zy < 0 –через квадраты I и III.