Построить эпюры изгибающего момента Mz и поперечной силы Qy.
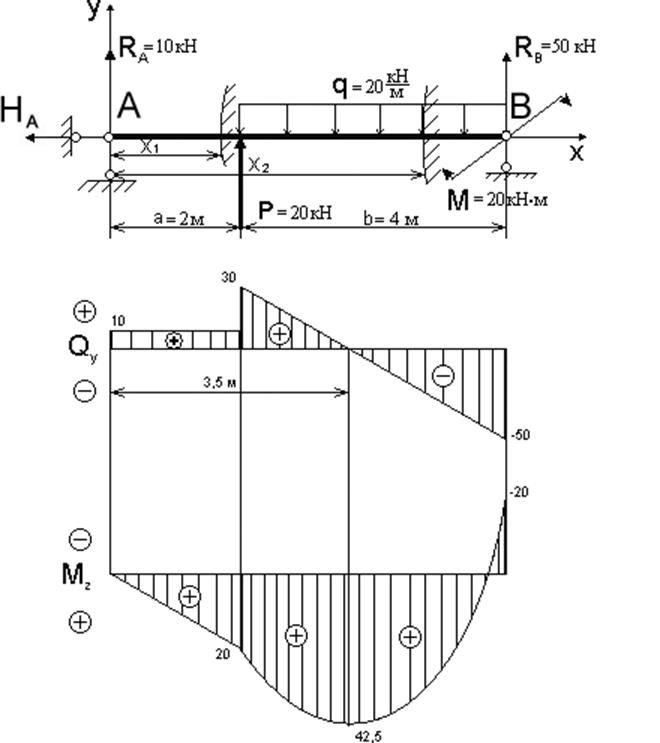
Рис. 1
1. Определение реакций.
Составим три уравнения равновесия статики и найдём RA и RB.
![]()
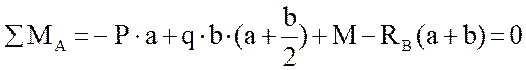
![]()
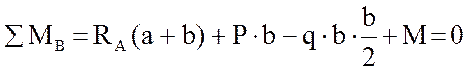
![]()
2. Построение эпюр Qy и Mz.
Балка по нагрузке имеет два участка.
Рассмотрим первый участок.
1-ый участок
![]()
Уравнение поперечной силы: ![]() (знак
«плюс», так как реакция создаёт момент относительно точки сечения по часовой
стрелке).
(знак
«плюс», так как реакция создаёт момент относительно точки сечения по часовой
стрелке).
Уравнение изгибающего момента ![]() (знак
«плюс», так как реакция создаёт момент относительно точки сечения с растянутыми
нижними волокнами). Mz зависит от
(знак
«плюс», так как реакция создаёт момент относительно точки сечения с растянутыми
нижними волокнами). Mz зависит от ![]() в первой степени. Для
построения прямой подставляем координаты
в первой степени. Для
построения прямой подставляем координаты ![]() в двух
точках:
в двух
точках:
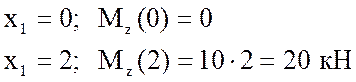
Рассмотрим второй участок.
2-ой участок
Запись уравнений на втором участке можно выполнить двумя способами: 1 – за начало отсчёта координаты x2 принимается точка А; 2 - за начало отсчёта координаты x2 принимается точка B.
1 вариант
![]()
Уравнение
поперечной силы: ![]() . Для построения эпюры необходимо
найти значения поперечной силы в крайних точках участка, так как Qyзависит
от x2в первой степени.
. Для построения эпюры необходимо
найти значения поперечной силы в крайних точках участка, так как Qyзависит
от x2в первой степени.
![]()
![]()
Уравнение
изгибающего момента: 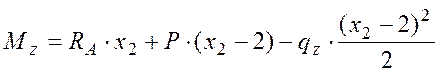 ,
,
где ![]() - результирующая сила на отрезке
- результирующая сила на отрезке ![]() ,
,
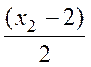 - расстояние от точки сечения до середины
отрезка
- расстояние от точки сечения до середины
отрезка ![]() .
.
![]() зависит от
зависит от ![]() в
степени 2.
в
степени 2.
Для построения эпюры необходимо три точки:
![]()
![]()
![]()
![]() определяется по условию экстремума
функции:
определяется по условию экстремума
функции: 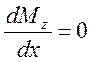
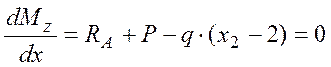
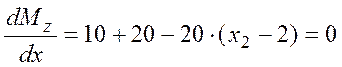 ,
,
отсюда
![]() .
.
Тогда
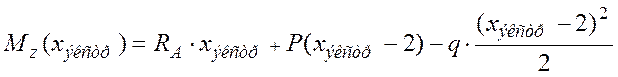
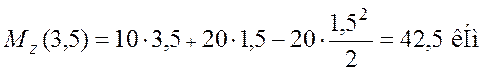 .
.
Второй
участок можно рассматривать от точки ![]()
2 вариант
![]()
Уравнение:
![]()
![]()
![]()
Уравнение:
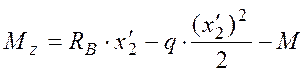 .
.
При
![]()
![]() .
.
![]()
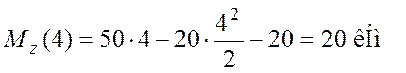
Для
определения ![]() необходимо найти
необходимо найти 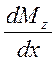
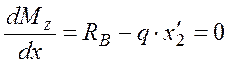
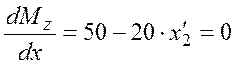
![]()
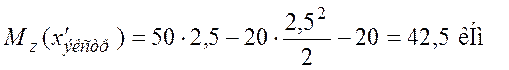
По найденным значениям построены эпюры на рис. 1.
3. Определение круглого стального сечения балки
Условие прочности имеет вид: 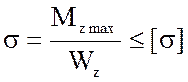 .
.
Момент сопротивления Wz для круглого сечения равен 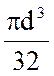 .
.
По построенной эпюре Mzmax= 42,5 кНм.
Допускаемое напряжение для стали Ст3 равно ![]() .
.
Тогда диаметр сечения 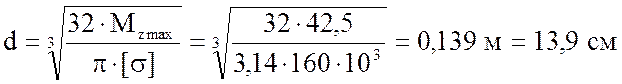 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.