|
Задание на контрольную работу за второй семестр
по теме: «Расчет на прочность и жесткость плоской статически определимой рамы»
Выбор исходных данных
Определение номера схемы
Если вторая цифра в учебном шифре четная, то первая цифра номер 0 (ноль), а если нечетная, то цифра 1.
Последняя цифра учебного шифра соответствует второй цифре номера схемы.
Например, если Ваш учебный шифр 7352, то номер схемы – 12, а если 6201, то номер 01.
В случае, если вторая цифра четная, а последняя цифра равна нулю, то выбирается номер схемы 20. Например, номер 6600.
В случае, если вторая цифра нечетная, а последняя цифра равна нулю, то выбирается номер схемы 10. Например, номер 6500.
Правила выбора длин участков
Длины участков определяются по цифрам учебного шифра:
обозначим первую цифру шифра за ш1, вторую – ш2, третью – ш3, четвертую – ш4. Так для шифра 7352 получаем ш1 = 7, ш2 = 3, ш3 = 5, ш4 = 2.
Длина первого участка l1 = 0,9 + ш1/10
Длина второго участка l2 = 1,5 + ш2/10
Длина третьего участка l3 = 1,3 + (ш3 + ш4)/10
Например, для шифра 7352 получаем:
Длина первого участка l1 = 0,9 + 7/10 = 1,6 м
Длина второго участка l2 = 1,5 + 3/10 = 1,8 м
Длина третьего участка l3 = 1,3 + (5 + 2)/10 = 2,0 м
Правила выбора внешних нагрузок
Внешние нагрузки определяются по цифрам учебного шифра:
Сосредоточенная нагрузка Р = 40 + ш2 + ш3
Распределенная нагрузка q = 20 + ш4·2 – ш3
Моментная нагрузка M = 100 – ш2 – ш4·2
Например, для шифра 7352 получаем:
Сосредоточенная нагрузка Р = 40 + 3 + 5 = 48 кН
Распределенная нагрузка q = 20 + 2·2 – 5 = 35 кН/м
Моментная нагрузка M = 100 – 3 – 2·2 = 93 кН·м
В расчете необходимо использовать только те нагрузки, которые указаны на расчетной схеме. Например, на схеме №2 учитывается только нагрузка q.
План расчета
1. Определение реакций в опорах. Для этого составляются суммы моментов относительно каждой опоры и суммы сил по горизонтальной и вертикальной осям.
2. Построение эпюр продольных усилий в стержнях рамы N, поперечных усилий Qy и изгибающего момента Mz. Для этого применяется метод сечений, далее расчет аналогичен расчету балки на изгиб за исключением, что знак изгибающего момента положителен в случае внутренних растянутых волокон. Для определения знака изгибающего момента необходимо обозначить геометрический центр рамы и при рассмотрении каждого сечения при растянутых волокнах ближних к центру рамы ставить знак «плюс» у соответствующего изгибающего момента и знак «минус», если растянутыми будут волокна дальние от центра рамы.
3. Проверка построенных эпюр. Для этого рассматриваются узлы рамы (узел рамы – это точка в которой соединяются два или более стержней). После переноса с эпюр N, Qy и Mz сил и моментов на узлы выполняется проверка условия статического равновесия. Для этого рассчитываются суммы сил по вертикальной оси, горизонтальной оси и сумма изгибающих моментов. Если все три суммы равны нулю, то эпюры построены верно. В противном случае необходимо искать ошибку в расчете реакций и внутренних усилий (N, Qy, Mz) на каждом участке.
4. Подбор сечения балки. Исходя из полученной эпюры Mz необходимо подобрать квадратное сечение для рамы. Для этого используется условие прочности при изгибе в которое входит максимальный изгибающий момент. Этот момент определяется из эпюры Mz и берется без учета знака (то есть если максимальный момент был -115 кНм, то в расчете поперечного сечения он берется как 115 кНм). Кроме условия прочности используется формула для расчета момента сопротивления при изгибе для квадратного сечения. Приравнивая момент сопротивления для квадратного сечения и момент сопротивления, необходимый по условию прочности, получаем уравнение, из которого можно определить сторону квадрата сечения.
5. Определение вертикального перемещения любой из двух левых точек рамы.
 |
|||||
 |
|||||
|
|||||
|
|||||
Для этого изображается вспомогательное состояние, в котором отсутствуют все внешние нагрузки, а в точке, где необходимо определить перемещение прикладывается единичная сила. Направить ее нужно вверх или вниз, так как определяется вертикальное перемещение. Для такого состояния строится эпюра изгибающих моментов (единичная эпюра). Далее необходимо перемножить эпюру изгибающих моментов Mz, полученную ранее, на полученную единичную эпюру. Перемножение необходимо осуществлять по правилу Верещагина или Симпсона (это зависит от формы эпюры изгибающих моментов Mz). Результат перемножения – величина перемещения в метрах.
Более подробное рассмотрение элементов расчета находится в указанных ранее учебниках и методических указаниях.
Расчетные схемы
(выбор по второй и четвертной цифрам учебного шифра)
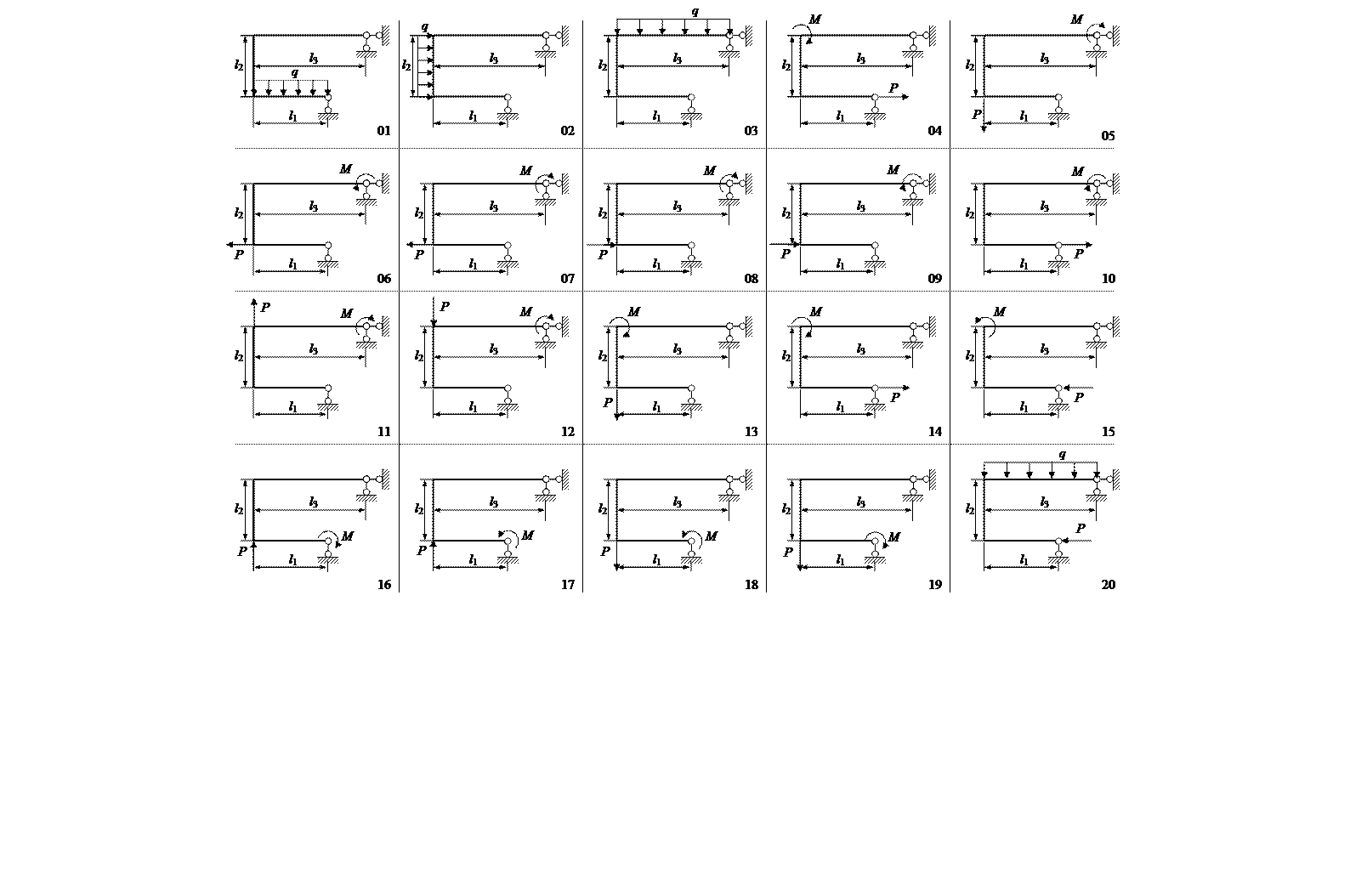
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.