Изгибом называется деформация стержня, сопровождающаяся изменением кривизны его оси. Стержень, работающий на изгиб, называется балкой.
В зависимости от способов приложения нагрузки и способов закрепления стержня могут возникать различные виды изгиба.
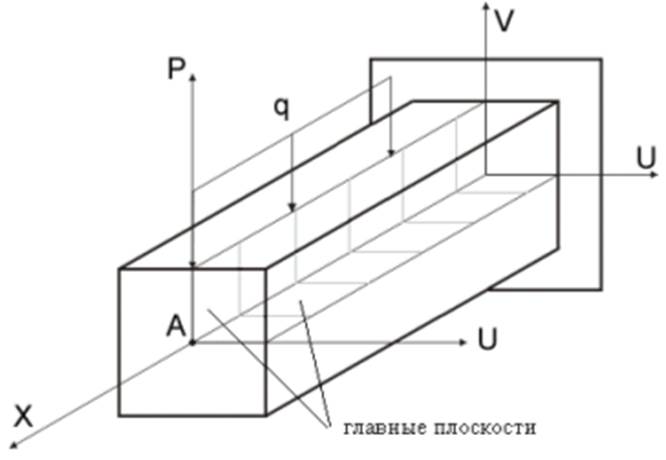
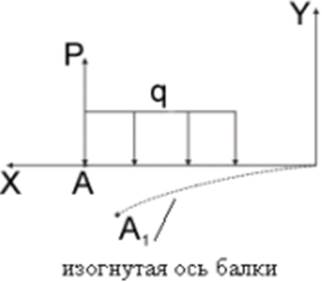
Если под действием нагрузки в поперечном сечении стержня возникает только изгибающий момент, то изгиб называют чистым.
Если в поперечных сечениях наряду с изгибающими моментами возникают и поперечные силы, то изгиб называют поперечным.
 |
|||
 |
|||
Чтобы балка могла воспринимать нагрузку в плоскости, она должна быть закреплена с помощью опор: шарнирно-подвижной, шарнирно-неподвижной, заделкой.
Балка должна быть геометрически неизменяемой, при этом наименьшее количество связей равно 3. Пример геометрически изменяемой системы приведен на рис.2а. Пример геометрически неизменяемых систем – рис. 2б, в.
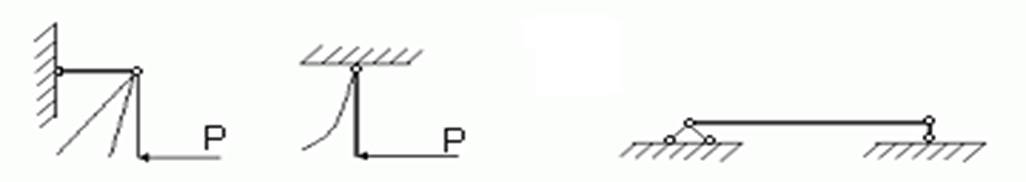 а) б) в)
а) б) в)
рис. 2
В опорах возникают реакции, которые определяются из условий равновесия статики. Реакции в опорах являются внешними нагрузками.
Стержень, нагруженный силами перпендикулярными продольной оси балки, испытывает плоский изгиб (рис. 3). В поперечных сечениях возникают два внутренних усилия: поперечная сила Qy и изгибающий момент Мz.
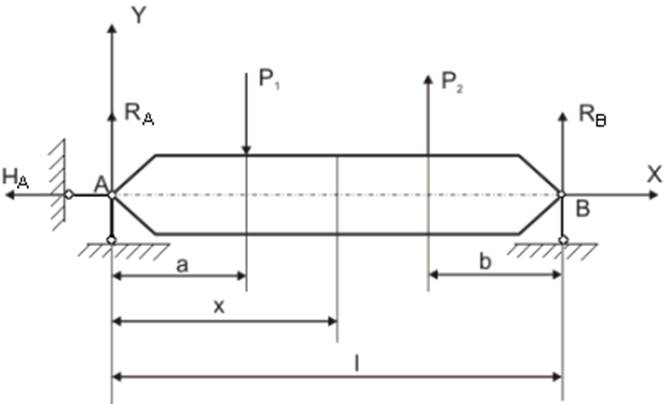 |
Определение реакций выполняется из условий равновесия:
из условия ∑x = 0 находится HA = 0;
из условий ∑MA = 0, ∑MB = 0 определяются RBиRA .
Проверка реакций в опорных стержнях вычисляется из условия ∑y = 0. Внешними нагрузками являются RA, RB, P1, P2.
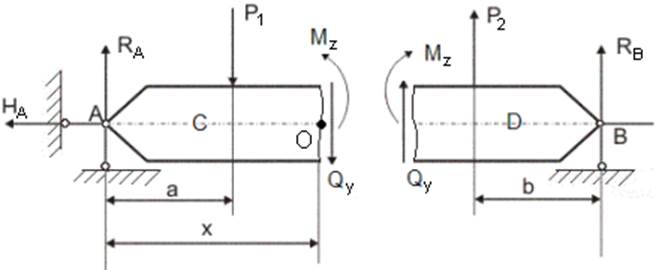 |
Рис. 4
Внутренние усилия Mz и Qy в сечение определяются из условий равновесия.
Составляется уравнение равновесия для части С:
∑y = RA – P1 – Qy = 0.
ТогдаQy = RA – P1.
Вывод. Поперечная сила в любом сечении балки равна алгебраической сумме всех внешних сил, лежащих по одну сторону от проведённого сечения. Поперечная сила считается положительной, если вращает стержень относительно точки сечения по часовой стрелке.
∑M0 = RA ∙ x – P1 ∙ (x - a) – Mz = 0
Тогда Mz = RA ∙ x – P1 ∙ (x – a)
 |
Построить эпюры Qy; Mzдля балки (рис.6).
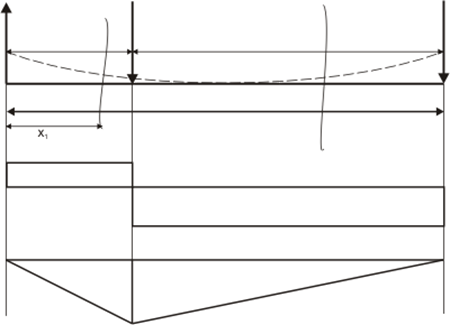 |
Рис. 6
1. Определение реакций RA , RB ;
∑MA = P ∙ a – RB ∙ l = 0
RB = ![]()
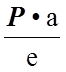
∑MB = RA ∙ e – P ∙ a = 0
RB = ![]()
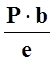
2. Построение эпюр на первом участке 0 ≤ x1 ≤ a
Qy = RA = 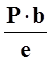 ; Mz = RA
∙ x1
; Mz = RA
∙ x1
x1 = 0 Mz(0) = 0
x1 = a Mz(a) = 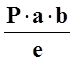
3. Построение эпюр на втором участке 0 ≤ x2 ≤ b
Qy = - RB = - 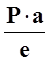 ; Mz = RB ∙ x2; x2 =
0 Mz(0) = 0 x2 = bMz(b) =
; Mz = RB ∙ x2; x2 =
0 Mz(0) = 0 x2 = bMz(b) = 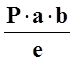
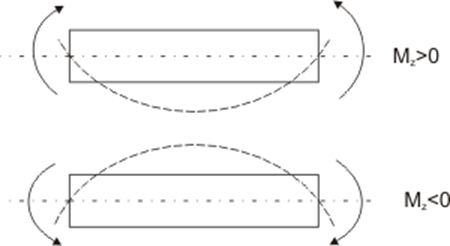
При построении Mzположительные координаты будут откладываться в сторону растянутых волокон.
1. На эпюре Qyразрывы могут быть только в местах приложения внешних сил и величина скачка должна соответствовать их величине.
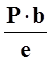 +
+
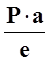 =
= 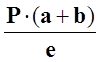 =
P
=
P
2. На эпюре Mzразрывы возникают в местах приложения сосредоточенных моментов и величина скачка равна их величине.
Дифференциальные зависимости между M, Q и q
Между изгибающим моментом, поперечной силой и интенсивностью распределённой нагрузки установлены зависимости:
q = 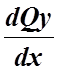 , Qy =
, Qy = 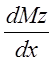
где q – интенсивность распределённой нагрузки,
Проверка прочности балок при изгибе
Для оценки прочности стержня при изгибе и подбора сечения балки используются условия прочности по нормальным напряжениям.
Изгибающий момент представляет собой равнодействующий момент нормальных внутренних сил, распределённых по сечению.
s = ![]() ×y,
×y,
где s – нормальное напряжение в любой точке поперечного сечения,
y– расстояние от центра тяжести сечения до точки,
Mz– изгибающий момент, действующий в сечении,
Jz– осевой момент инерции стержня.
Для обеспечения прочности рассчитываются максимальные напряжения, которые возникают в точках сечения, наиболее удалённых от центра тяжести y = ymax
smax = ![]() ×ymax,
×ymax,
где
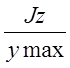 = Wz
и smax =
= Wz
и smax = ![]() .
.
Тогда условие прочности по нормальным напряжениям имеет вид:
smax = ![]() ≤ [s],
≤ [s],
где [s] – допускаемое напряжение при растяжениях.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.