Методика подбора поперечного сечения гибкого сжатого стержня

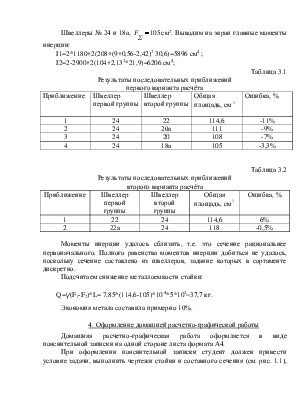
1.  Методика подбора поперечного сечения гибкого сжатого стержня

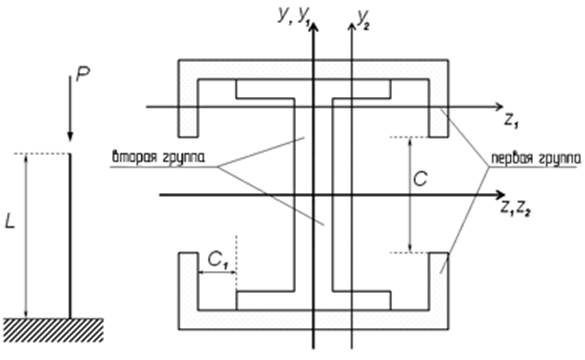
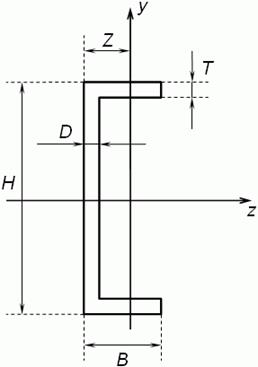
   рис. 1.1. Стойка и её поперечное сечение                               рис 1.2. Швеллер

В качестве сложного, составного сечения, подбираемого в индивидуальном домашнем задании, рассматриваются симметричные сечения, составленные из двух типов простых фигур (комбинации уголков, двутавров, швеллеров, полос). Варианты индивидуальных заданий приведены в приложении данных методических указаний.

Подбор поперечных сечений сжатых стержней выполняется методом последовательных приближений. Сечение считается подобранным, если с пятипроцентной точностью (перегрузка или недогрузка не более 5%) выполняется условие устойчивости:

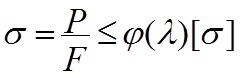
где s - нормальное напряжение в сечении стержня;

Р– осевая сжимающая нагрузка;

F – площадь поперечного сечения;

j(l) – коэффициент уменьшения допускаемых нормальных напряжений [s] материала стержня, зависящий от его гибкости l.

В дальнейшем методика расчета изложена для одного конкретного сечения.

1.1. Условие задания и порядок расчета

Подобрать сечение стойки из четырех одинаковых швеллеров (рис. 1.1.), если Р=900 кН; L=4м; [s]=160 * 10³ кПа.

Подобрать поперечное сечение – это значит указать необходимый номер швеллера, который определяет и все основные размеры: H, D, Z, B, T (рис.1.2) и геометрические характеристики: площадь сечения F, осевые моменты инерции J_Z и J_Y, обозначенные J1 и J2.

 В первом приближении принято назначать коэффициент уменьшения основного расчетного сопротивления j=0,5 и определять общую площадь сечения согласно (1.1) по формуле:

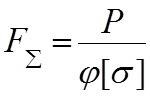                                                   .                                                               (1.2)

Тогда площадь одного швеллера

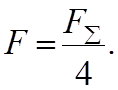                                                                                                                 (1.3)

Затем для составленного сечения последовательно находят:

·  осевые моменты инерции –

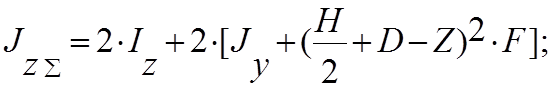
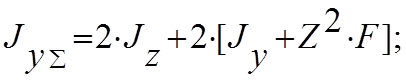
·  радиус инерции сечения –

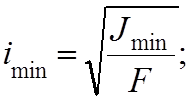
·  гибкость стержня –

.

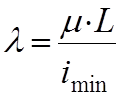В качестве Jmin выбирается наименьший момент инерции из Jzå  , Jyå_.  В формуле (1.7) m – коэффициент приведения длины, учитывающий характер закрепления концов стойки, в программе обозначен M.

По найденной гибкости l вычисляют новое, уточненное значение коэффициента уменьшения основного расчетного сопротивления j_1. Обычно величину j определяют с помощью специально составленных таблиц. Поскольку в приводимом расчете предполагается использование ЭВМ, приведем аналитические зависимости, позволяющие находить j₁:

Результаты расчета оцениваются по значению ошибки между действительными напряжениями s_д в стойке и допускаемыми напряжениями устойчивости j_1* [s]:

Если ошибка превышает 5%, то для второго приближения выбирается

и расчет повторяется.

Действительное напряжение в стойке

2. Структурно-параметрическая схема алгоритма решения и подготовка задачи к диалоговому режиму работы на ЭВМ.

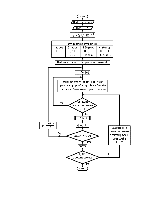
Структурно-параметрическая схема алгоритма решения, соответствующая методике расчёта, изложенной в разд. 1, приведена на рис.2.1.

Имея целью освободить студента от набора всех размеров и геометрических характеристик прокатных профилей, которые используются при решении задачи, в память машины введён сортамент прокатных профилей, и студенту достаточно указать лишь номер профиля.

Студент вводит значения нагрузки p, длины стойки L и коэффициента закрепления концов стержня M.

Выше отмечалось, что в задании предложены только симметричные сечения, состоящие из двух типов простых сечений. В нашем конкретном случае (см. рис. 1.1) хотя сечение состоит из четырёх одинаковых швеллеров, программа требует разбиения их также на две группы.

Отнесём к первой группе горизонтально расположенные швеллеры и для обозначения размеров и геометрических характеристик сечения используем символы:

H (Ø), B (Ø), D (Ø), T (Ø), Z (Ø), F (Ø), J1 (Ø), J2 (Ø). 

Ко второй группе отнесём вертикальные швеллеры, для которых введём обозначения:

H (1), В (1), D (1), T (1), Z (1), F (1), J1 (1), J2 (1).

Соответствующие коды первой и второй групп элементов сообщаются ЭВМ.

Поскольку не при любых произвольных размерах сечение, изображенное на рис. 1.1, может быть реализовано, следует сформулировать условия реальности сечения. В рассматриваемом конкретном варианте сечения такими условиями являются:

C>0 и C1>0.

Эти условия автоматически проверяются программой, и соответствующий анализ выдается на экран дисплея. Однако предварительно студент должен записать на языке Бейсик аналитические выражения для соответствующих условий и набрать их с клавиатуры как команды с номерами 385 и 386. В приводимом примере эти команды будут выглядеть следующим образом:

385 c=h(1)+d(Ø)*2–2*b(Ø)

(2.4)

386 c1=h(Ø)/2–b(1)–t(Ø)