Количественное оценивание ИС. Формальная модель ИС, определение энтропии по Хартли и Шеннону. Свойства энтропии. Полная и условная энтропия и их свойства

Количественное оценивание ИС. Формальная модель ИС, определение энтропии по Хартли и Шеннону. Свойства энтропии. Полная и условная энтропия и их свойства

В теории информации рассматривается неэнергетическое взаимодействие 2-х и более объектов. Рассмотрим классический пример передачи информации:

 

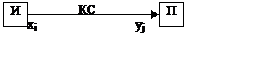И – источник, П – приемник, КС – канал связи.

Рисунок 1.1 – Модель передачи информации.

Информация переносится с помощью сигналов, т.е. изменения некоторых физических параметров в канале связи. Основной вид КС – эл.-маг. поле (его изменение).

Для того, чтобы приемник получил информацию от источника необходимо, чтобы он ее не имел до сих пор. Т.о. для передачи информации необходимо, чтобы источник имел некоторую неопределенность относительно приемника. Чем больше эта неопределенность, тем большее количество информации может быть передано.

Для получения информации от источника, необходимо приемнику знать природу её хранения и извлечения.

Т.о. необходимо научиться описывать неопределенности. Предположим, объект имел N различных состояний, каждое следующее состояние неизвестно. Чтобы описать неопределенность, нужна функция f(N). Эта функция называется энтропией f(N) - мера неопределенности. Необходимо сформулировать требования к этой функции при условии, что N – конечно:

1. функция должна быть определена для положительных N;
2. функция должна быть монотонно возрастающей (N₂>N₁; f(N₂)>f(N₁));
3. При N=1 f(1)=0;

N=N₁*N₂ – пары этих объектов должны соответствовать сумме неопределенностей, где f(N₁N₂)=f(N₁)+f(N₂).

Формула энтропии по Хартли: H(x)=log_aN.

В зависимости от а различают различные единицы измерения:

а=2     бит;         а=е     нит;         а=2     дит.

Основной недостаток формулы Хартли: она не учитывает вероятности состояния объекта.

Предположим, что источник информации генерирует последовательность символов какое-то время наблюдения Т. За время Т сгенерирована N-последовательность символов, среди них первый появился n₁ раз, второй – n₂ и т.д.

υ=n_k/N_T – частота = количество наблюдаемых символов / длина общей последовательности.

Источник сообщений называется эргодическим, если относительная частота появления символов приближается к их вероятности. Большинство естественных текстов является эргодическими.

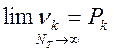    P(x_k)

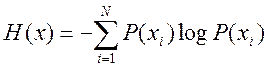 (1) - Формула энтропии по Шеннону

Свойства энтропии по выражению (1):

1. эта функция, от аргумента Р – непрерывна;
2. энтропия максимальна, если все исходы равновероятны. Следовательно, энтропия по Хартли – есть верхняя оценка энтропии по Шеннону

H=-p*logP-(1-p)*log(1-p)

3. при увеличении N – энтропия возрастает;
4. энтропия не отрицательна;
5. при вычислении энтропии по (1) маловероятные события можно не учитывать.

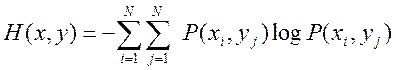 - полная энтропия.

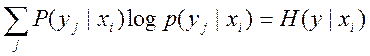 - частота установления энтропии.

Член 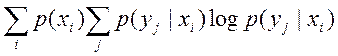 есть мат. ожидание частных условных энтропий и он носит название условная энтропия.

H(x,y)=H(x)+H(y) (2.1) – x и y независимы;

H(x,y)=H(x)+H(y|x) (2.2) – x и y зависимы;

H(x,y)=H(y)+H(x|y).

Условная энтропия максимальна и равна H(y), в случае независимости х и у. Отсюда полная энтропия так же максимальна в случае независимости.

Свойства полной энтропии:

1. она максимальна при независимости х и у и равна H(x)+H(y);
2. из основного уравнения (2) следует, что она не отрицательна при любых р;
3. минимальное значение полной энтропии соответствует жесткой зависимости У(х), тогда H(X,Y)=H(x)

Свойства условной энтропии:

1. H(Y|X)=0 при жесткой зависимости У(Х);  Р(У_i|X_i)=1|_i
2. При независимости у(х): H(Y|X)=H(Y)
3. H(Y|X) по х не отрицательна.
4. 0≤H(X|Y) ≤H(X).

Полная энтропия отражает общую неопределенность некоторой объединенной ИС, в т.ч. с несвязанными источниками/приемниками. Условная энтропия ориентирована непосредственно на взаимодействующие подсистемы. Если речь идет о передаче информации, то идеальным будет считаться взаимодействие, когда условная энтропия равна нулю. Любая энтропия максимальна при равновероятных исходах, маловероятные события не учитываются при вычислении энтропии.

2. Количество информации, его свойства. Энтропия и информационные свойства непрерывных источников. Матричное описание информационных каналов. Матрицы совместных вероятностей и канальные матрицы.

Рассмотрим модель информационного канала (см. рис. 1.1). Предположим, приемник принял одно сообщение. Тогда неопределенность источника относительно приемника при этом снижается, и на такую же величину приемник приобретает информацию. Это приращение количества информации в приемнике:

D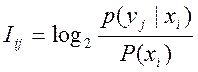

Для того, чтобы получить усредненное значение количества информации, необходимо усреднить полученную оценку по всем i, j (т.е. взять мат. ожидание).

           

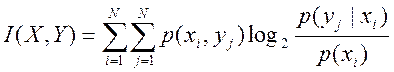
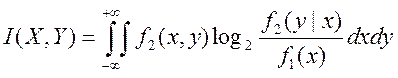
Где I – количество информации, N – количество возможных событий, рⁱ – вероятности отдельных событий.

Количество информации, которое мы получаем, достигает максимального значения, если события равновероятны.

Таким образом, количество информации есть среднее значение изменения неопределенности в приемнике на один символ.

I(X,Y)=H(X)-H(X|Y);            I(X,Y)=H(Y)-H(Y | X)   (*)

I(X,Y)=H(X)+H(Y)-H(X,Y) – симметричная форма количества информации.

Свойства количества информации: