Количественное оценивание ИС. Формальная модель ИС, определение энтропии по Хартли и Шеннону. Свойства энтропии. Полная и условная энтропия и их свойства, страница 2

1. количество информации максимально и равно Н(Х): I(X,Y)=H(Х) при жесткой зависимости Х и У.
2. минимальное количество информации I(X,Y)=0 при независимости Х и У.
3. количество информации величина не отрицательная.
4. остальные свойства I(X,Y) переносятся из свойств энтропии H(X).

Максимальное количество информации возможно при равновероятных исходах источника. Второй член этого выражения (*), т.е. H(X|Y) – это потеря информации. Она может быть вызвана помехами, потерями преобразований при восстановлении и т.д. В любом случае, процесс передачи информации – это единое гармоническое целое из источника, приёмника и канала связи.

Свойства количества информации:

1. количество информации определяет среднее её значение на одно событие от источника.
2. эта оценка объективна и носит чисто формальный характер.
3. информационное взаимодействие присуще в основном живым организмам и представляет собой высшую форму взаимодействий, известных на сегодня.

За единицу количества информации принята величина ин­формации, содержащейся в сообщении об одном из двух равновероятных событий.

Единица измерения количества информации

За единицу количества информации принято такое количество информации, которое содержит сообщение уменьшающее неопределённость знания в 2 раза. Такая единица названа бит.

Компьютер оперирует числами в двоичной системе счисления, поэтому в кратных единицах измерения количества информации используется коэффициент 2n.

Следующей по величине единицей измерения количества информации является байт, причём

1 байт = 2³ бит = 8 бит.

Кратные байту единицы измерения количества информации вводятся следующим образом:

1 Кбайт = 210 байт = 1024 байт

1 Мбайт = 210 Кбайт =1024 Кбайт = 220 байт

1 Гбайт = 210 Мбайт = 1024 Мбайт = 220 Кбайт = 230 байт.

Количество возможных событий и количество информации

Существует формула, которая связывает между собой количество возможных событий N и количество информации I:

N=2^I

Энтропия неперерывных сообщений:

Любой отрезок конечной длины L имеет бесконечное множество внутренних точек. С отрезком отождествляется физ. параметр, поддающийся измерению. Необходимо определить количество информации, получаемое от этого измерения. Для этого разделим интервал длины L на N равных частей. Если вероятности попадания в каждый интервал одинаковы, то энтропию можно определить следующим образом:

H(x)»log₂N= log₂(L/DL), где DL – погрешность измерений, длина отрезка одного деления. Это выражение эквивалентно энтропии по Хартли. Фактически эти события не равновероятны, поэтому запишем выражение по Шеннону:

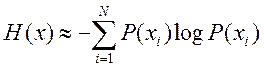
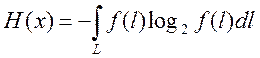, где l – текущий параметр длины, f(l) – плотность распределения вероятности. Одномерная плотность распределения вероятностей графически представляется в виде плоскости, двумерная – в виде поверхности.

В инф. системах непрерывного действия необходимо учитывать источник и приемник, для этого вводится двумерная плотность распределения вероятностей. Она описывает поверхность распределения вероятностей 3-х мерного пространства, подчиняется формуле Байеса: f₂(x,y)=f₁(x)f₂(y|x).

Пользуясь аналогией для дискретных событий запишем: 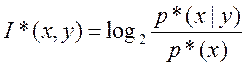, где р* - интервальные вероятности. Проинтегрируем по всем возможным вероятностям.

, I(X,Y)=H(X)-H(X|Y

,

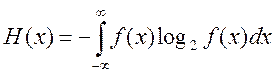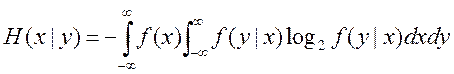
Потери информации возникают вследствие ограниченной точности преобразования (внутренняя нестабильность объекта) и помех.

Н_e(х) – эпсилон-энтропия (e-энтропия) соответствует минимальному количеству информации, которую необходимо получить от объекта для определения его параметра (состояния) с точностью e.