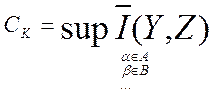Количественное оценивание ИС. Формальная модель ИС, определение энтропии по Хартли и Шеннону. Свойства энтропии. Полная и условная энтропия и их свойства, страница 4

 - пропускная способность канала.

Значительная часть ограничений, снижающих поток информации, определяется необходимостью повышения помехоустойчивости. Вторая часть ограничений связана с особенностями канала. Поток информации пропорционален полосе частот канала: , бит/с »Гц.

Для нормальной работы системы: С_К>С.

Теорема Шеннона для дискретных каналов без шумов.

Если пропускная способность системы , e - бесконечно малая величина, то существует способ передачи, обеспечивающий передачу всех сообщений без искажений.

Обратная теорема.

Если , то не существует способа передачи.

Если пропускной способности не достаточно, то потеря информации неизбежна.

Теорема Шеннона для дискретных каналов с шумами.

Если пропускная способность , то существует способ передачи, обеспечивающий передачу всех сообщений без искажений.

Для борьбы с помехами используют одну из форм избыточности: по амплитуде, по мощности, по времени, по информации. Реальный поток информации при этом снижается.

Обратная теорема.

Если , то потеря информации неизбежна.

Теорема Шеннона для непрерывных каналов.

|x_min------------------------à|Δx|ß---x_max|  

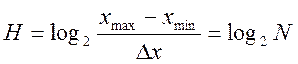
Если увеличивать точность измерения, то Δx – уменьшается и соответственно количество информации возрастает.

Информационный ресурс непрерывных параметров бесконечен.

ε-энтропия (H_ε(x)) соответствует минимальному количеству информации, получаемой от объекта для определения его состояния с точностью ε.

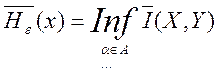
Если пропускная способность инф. системы равна , где  - поток ε-энтропии, a- бесконечно малая величина, то существует способ передачи, обеспечивающий передачу всех сообщений без искажений.

Обратная теорема: Если это условие не выполняется, то не существует способа передачи всех сообщений без искажений.

Теорема Шеннона с шумами.

Если , то существует способ передачи, обеспечивающий передачу информации без искажений.

Если энтропия источника сообщений не равна максимальной энтропии для алфавита с данным количеством качественных при­знаков (имеются в виду качественные признаки алфавита, при помо­щи которых составляются сообщения), то это прежде всего означает, что сообщения данного источника могли бы нести большее количество информации. Абсолютная недогруженность на символ сообщений такого источника

Для определения количества «лишней» информации, которая заложена в структуре алфавита либо в природе кода, вводится понятие избыточности. Избыточность, с которой мы имеем дело в теории информации, не зависит от содержания сообщения и обычно заранее известна из статистических данных[1]. Информационная избыточность показывает относительную недогруженность на символ алфавита и является безразмерной величиной:

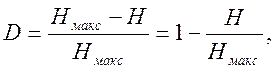                                                    (хх)

где 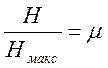— коэффициент сжатия (относительная энтропия). и  берутся относительно одного и того же алфавита.

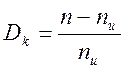Избыточность — не всегда нежелательное явление. Для повышения помехоустойчивости кодов избыточность необходима и ее вводят искусственно в виде добавочных  символов (см. тему 6). Если в коде всего п разрядов и  из них несут информационную нагрузку, то =  характеризует абсолютную корректирующую избыточность, а величина  характеризует относительную корректирующую избыточность.

Информационная избыточность - обычно явление естественное, заложена она в первичном алфавите. Корректирующая избыточность - явление искусственное, заложена онав кодах, представленных во вторичном алфавите.

Наиболее эффективным способом уменьшения избыточности сообщения является построение оптимальных кодов.