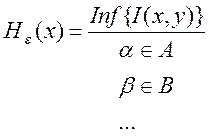Количественное оценивание ИС. Формальная модель ИС, определение энтропии по Хартли и Шеннону. Свойства энтропии. Полная и условная энтропия и их свойства, страница 3

, где Inf (инфинум) – наименьшее значение, aÎА, bÎВ, … - формальная запись ограничений во времени измерений.

Матричное описание свойств информационного канала.

Описание инф. каналов производится заданием системы вероятностей. Простейшее описание для источников – это таблица:

К	1	2	3	…	N
Рк	Р1	Р2	Р3	…	РN

Использование матричного описания позволяет решить следующие задачи:

1. По матрице совместных вероятностей определить все виды энтропии

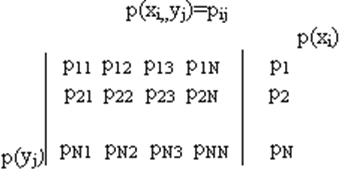
H(x,y)=-Σ_i Σ_j p_ij log p_ij

H(x)= -Σ_i p_i log p_i

H(y)= -Σ_j p_j log p_j

H(x,y)=H(x)+H(y|x),

следовательно, H(y|x)=H(x,y)-H(x),

следовательно, H(y|x)=H(x,y)-H(y).

Все значения должны быть положительными.

Матрица имеет вероятностный характер, т.е. их члены состоят из вероятностей.

2. Канальные матрицы – это матрицы условных вероятностей P(y_j|x_i) или P(x_i|y_j). P(x_i|y_j): источник передает x_i, приемник, получая y_j, восстанавливает по ним x_i. P(y_j|x_i): источник, передавая x_i, оценивает вероятность их восстановления.

    

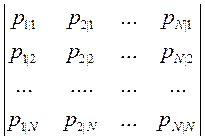
Идеальный вариант при полной вероятности будет единичная матрица. Во всех других случаях это ленточная матрица типа Ганкеля.

Возможны канальные матрицы относительно передающей части. Они отличаются тем, что сумма вероятностей равна 1 по столбцам. Канальная матрица недостаточна для вычисления количества информации, ее нужно дополнять матрицей-столбцом вероятностей отдельных символов. Результат не должен быть отрицательным.

Особенности -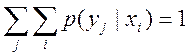

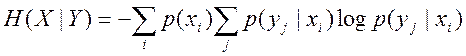
3. Поток энтропии и информации. Пропускная способность, избыточность сообщений, использование избыточности. Связь потока информации с полосой частот. Ограничение Найквиста. Теорема Шеннона для дискретных каналов с шумами и без шумов. Теоремы Шеннона для непрерывных каналов.

Предположим, источник последовательно во веремни принимает случайные значения из множества возможных N. Предположим, источник наблюдается время Т, а среднее время пербывания его в таком состоянии τ. За время т будет получено s символов. S=Т/ τ. Относительное появление каждого символа: n_i=s_i/S.

Эргодическими называются последовательности, в которых при неограниченном увеличении Т, относительные частоты символов (состояний) стремятся к их вероятностям.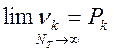

Эргодическая последовательность однородна во времени. Для эргодических источников можно вычислить вероятность каждого из состояний, следовательно, вычислить энтропию и кол-во информации, приходящиеся на 1 символ. Предположим далее, что символы друг от друга не зависят. Пусть энтропия одного состояния равна Н(х), то за время Т Н_Т(х)=S* Н(х). (Если символы зависят друг от друга, общее значение уменьшается).

Потоком энтропии называется ее среднее значение за 1 времени.

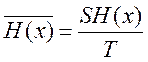, бит/с (бод)

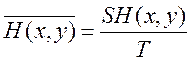 - поток полной энтропии,

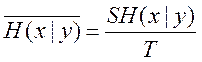- поток условной энтропии.

Предположим каждый символ источника генерируется через интервал τ, тогда можно взять следующую оценку H(x)/τ = поток энтропии =

Поток энтропии характеризует скорость передачи сообщения от источника:

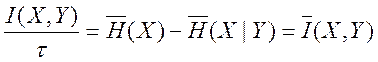 - поток информации.

Предположим, что информация передается 0 и 1, тогда для пердачи 1 бита информации требуется минимум 1 символ.

Предположим, что импульс передается первыми гармониками, следовательно, 1 бит будет соответствовать основной частоте.

 - ограничение Найквиста.

(И)-----^Х-----[M]----- ^Y ----кс-----|^П----^Z---[ДМ]---^W---(П)

И – источник;

М – модулятор;

кс – канал связи;

ДМ – демодулятор;

П – приемник.

|^П - помеха

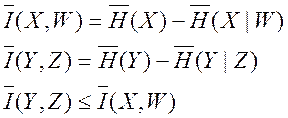
(часть информации может теряться в канале связи)

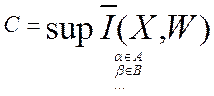 - пропускная способность соответствует максимальному потоку информации в этой системе с учетом фиксированных ограничений.