Определим для этого цикла его термодинамический КПД, или иначе называемый термический.
Как мы уже видели, все количество
тепла подводится в процессе 1-2 изотермического расширения. Это количество
тепла мы обозначим через q1. Очевидно, количество отведенного
тепла q2 меньше величины q1, ибо согласно I-му
закону термодинамики, нельзя было бы получить полезную работу цикла, выражаемую
пл. 1-2-3-4-1, т.е. q1 – q2 = 
, где выражается пл.
1-2-3-4-1.
Следовательно, термический КПД может быть выражен:
.
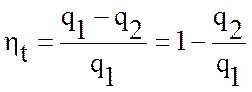В 1824 году Карно доказал, что КПД идеальной тепловой машины зависит только от абсолютных температур двух источников тепла, поэтому он может быть выражен:
.
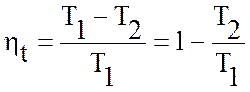Например, при стандартной абсолютной температуре поступающего в турбину пара Т1 = 565 + 273 = 838 К и абсолютной температуре в конденсаторе Т2 = 30 + 273 = 303 К потери составят:
303: 838 = 0,36, т.е. 36 %,
а КПД идеальной тепловой машины, работающей при таких условиях, не может быть выше
1– 0,36 = 0,64, т.е. 64 %.
Карно показал таким образом, что даже в идеальной машине неизбежна потеря тепла в холодном источнике. В нашем примере эта потеря составляет 36 %, т.е. более 1/3 части тепла выделившегося при сжигании топлива.
Контрольные вопросы для самопроверки
1. В чем заключается сущность второго закона термодинамики?
2. Дать некоторые формулировки второго закона термодинамики.
3. Что называется круговым процессом или циклом?
4. Из каких процессов складывается цикл Карно? Как он отображается в диаграмме V-P?
5. Чему равен термический КПД цикла Карно?
6. Почему КПД цикла Карно не может быть равен единице?
2.2. Водяной пар
Наибольшее применение в технике имеет водяной пар, являющийся рабочим телом паровых машин, паровых турбин и других отопительных устройств.
Законы, относящиеся к идеальному газу, можно распространить и на водяной пар, так как водяной пар – это газ.
Если уравнение для идеального газа, известное под названием уравнения Клайперона-Менделеева, записывалось как
PV=RT,
то уравнение для водяного пара не применимо, так как в водяном паре должно учитываться влияние сил взаимодействия молекул и влияние объема молекул.
Для водяного пара предлагалось уравнение Ван-дер-Ваальса (голландский ученый)
.
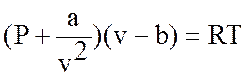В этом уравнении не одна постоянная величина R, а три – a, b и R.
В уравнении идеального
газ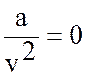а 
(отсутствие силы взаимодействия молекул) и
b = 0 (отсутствие влияния объема).
Очень большую работу провели советские ученые М. П. Вукалович и Н. И. Новиков, разработавшие уравнение состояния реального газа. Но им пользоваться в практической жизни трудно и они разработали для водяного пара систему таблиц и h-S диаграмму, характеризующие состояние водяного пара при любом термодинамическом процессе.
Процесс преобразования в диаграмме V-P
Чтобы легче рассмотреть процесс парообразования, возьмем 1 кг воды при t = 0 оС, нальем ее в цилиндрический сосуд и накроем его поршнем, вес которого равен Gкг (рис. 2).
Допустим этот вес создает давление Р1.
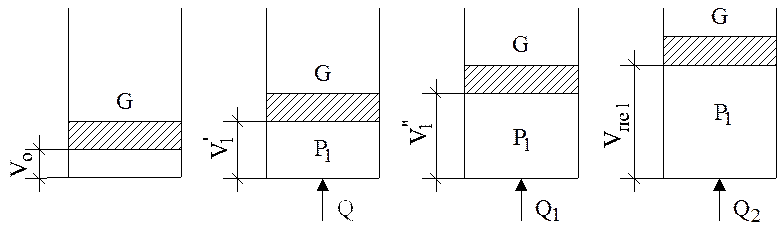
Рис. 2. Процесс расширения пара при Р = const
При t = 0 оС вода занимает объем, равный v = 0,001 м3. Допустим это состояние воды отображается на рис. 2, а.
Будем ставить на поршень различные грузы и заметим, что объем воды не меняется. Следовательно, воду можно принять за несжимаемую жидкость. Изобразим координаты P-V диаграммы (рис. 3).
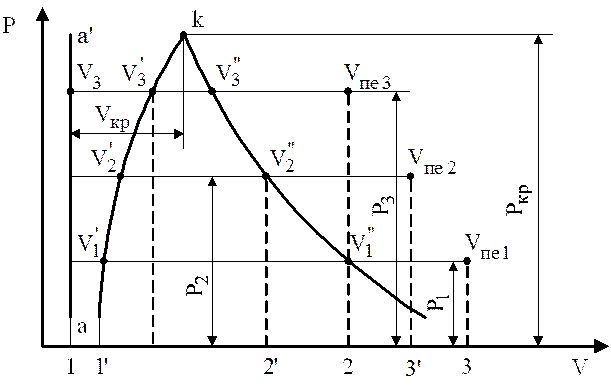
Рис. 3. Процесс парообразования в P-V диаграмме
Отложим на P-V диаграмме объем, равный 0,001 м3, и поскольку при любом давлении объем остается неизменным, то на диаграмме это изобразится прямой а–аp.
Начнем воду в цилиндре постепенно нагревать, не снимая с нее поршня, т.е. будем осуществлять изобарный процесс нагрева воды, при этом заметим, что температура воды и ее объем будут постепенно возрастать.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.