



Лекція 5
План.
1. Інтегрування тригонометричних функцій і деяких ірраціональних.
Функцію з
перемінними ![]() , над якими виконуються раціональні дії
(додавання, вирахування, множення, розподіл) прийнято позначати
, над якими виконуються раціональні дії
(додавання, вирахування, множення, розподіл) прийнято позначати ![]() , де R – знак раціональної функції.
, де R – знак раціональної функції.
Якщо функція ![]() не є парною, тобто
не є парною, тобто
![]() ,
,
то вводиться підстановка 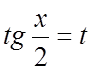 , і тоді
, і тоді 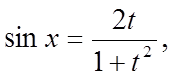
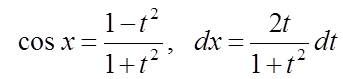 .
.
Якщо функція R – парна, то
простіше застосувати підстановку ![]() , і тоді
, і тоді 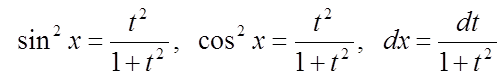 .
.
Інтеграли
типу 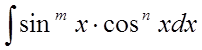
1. Якщо одна з функцій стоїть в непарному ступені, то з непарного ступеня виділяється перший ступінь і робиться підстановка.
Наприклад:

Також вирішуються інтеграли, якщо під знаком інтеграла в чисельнику стоїть тригонометрична функція в непарному ступені, а в знаменнику – будь-який ступінь тригонометричної функції.
Наприклад:
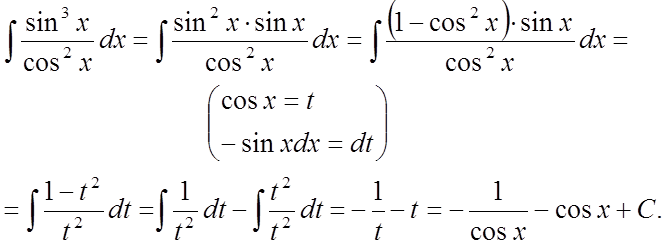
2. Якщо ступеня тригонометричних функцій позитивні і парні, то використовуються формули зниження порядку:
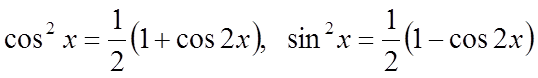 .
.
Наприклад:
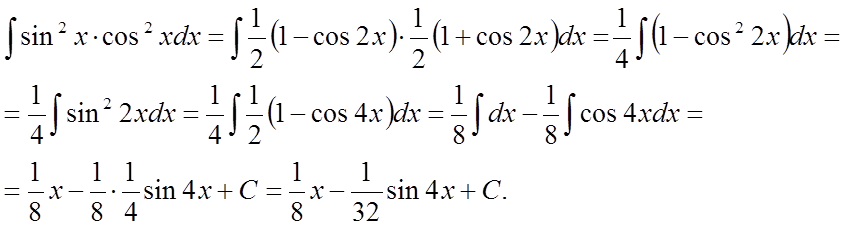
3. Інтеграли
типу 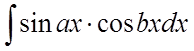 ,
, 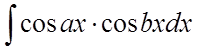 ,
, 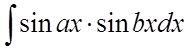 обчислюються за допомогою відомих формул
тригонометрії:
обчислюються за допомогою відомих формул
тригонометрії:
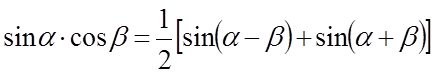 ,
,
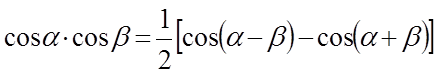 ,
,
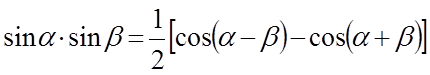 .
.
Наприклад: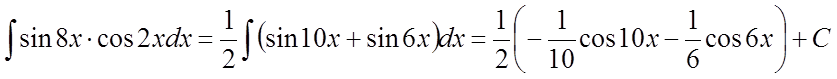 .
.
Інтеграли виду:
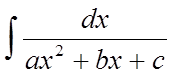 ,
, 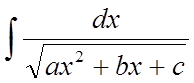 ,
, 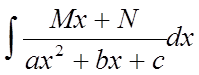 ,
, 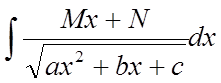
Щоб вирішити
інтеграли такого виду, варто виділити повний квадрат знаменника і ввести нову
перемінну, позначивши ![]() , за допомогою якої інтеграли
зводяться до табличного.
, за допомогою якої інтеграли
зводяться до табличного.
Приклади.
1. Знайти 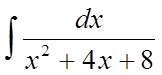 .
.
Виділимо в знаменнику повний квадрат:
![]() , тому що
, тому що
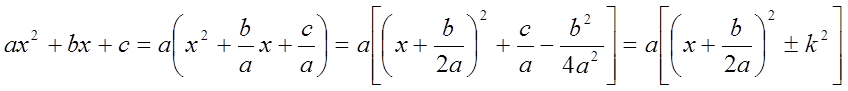 .
.
Тоді 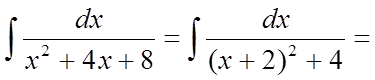
(позначимо
![]() )
)
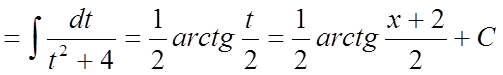 .
.
2. 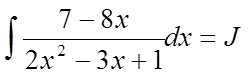 .
.
Виділимо повний квадрат у знаменнику:
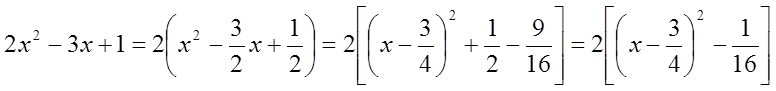
і покладемо 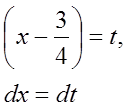 ,
,
тоді одержимо
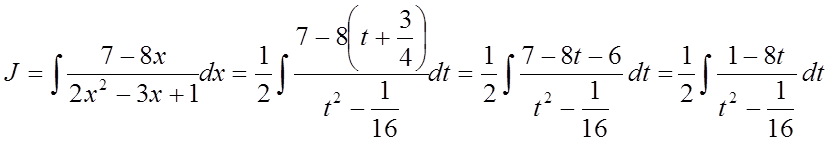 .
.
Далі розкладемо отриманий інтеграл на дві складові інтегралиу відповідно двом доданкам у чисельнику і знаходимо них за формулами:
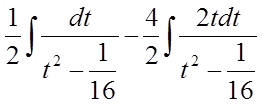 .
.
Перший інтеграл табличний, а в другому інтегралі в чисельнику добудуємо похідну знаменника і застосуємо табличну формулу інтегралів:
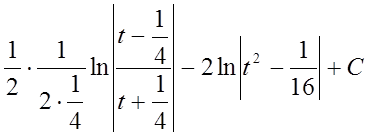 .
.
Повертаючи до перемінного х, остаточно одержимо
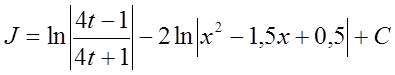 .
.
3.
Знайти 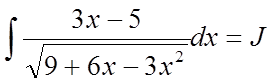 .
.
Виділимо повний квадрат знаменника:
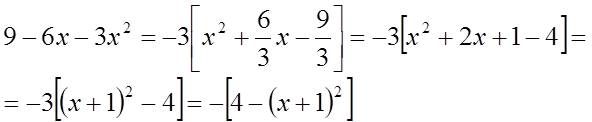
і зробимо підстановку:
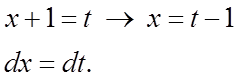
Одержимо: 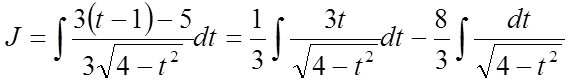 .
.
У першому інтегралі в чисельнику добудуємо похідну підкореневого вираження, а другий інтеграл табличний. Остаточно одержимо:
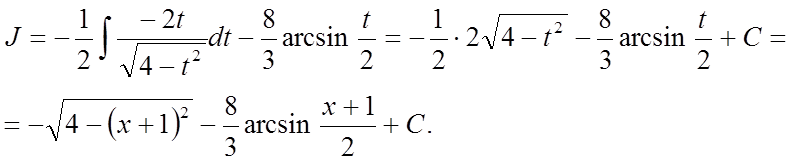
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.