




Лекція 7
План.
1. Формула Ньютона-Лейбніца.
2. Методи обчислення визначеного інтегралу.
3. Невласні інтеграли
1. Формула Ньютона-Лейбніца
Нехай функція ![]() безперервна на відрізку
безперервна на відрізку ![]() і
і ![]() –
яка-небудь її первісна на
–
яка-небудь її первісна на ![]() , тоді має місце формула
, тоді має місце формула
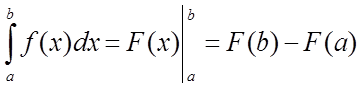 ,
,
яка називається формулою Ньютона-Лейбница і служить для обчислення визначеного інтеграла.
Наприклад, 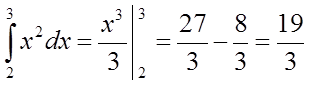 .
.
2. Методи обчислення визначеного інтегралу
Формула Ньютона-Лейбница дає загальний метод обчислення визначених інтегралів, що складає в тім, що для даної безперервної функції знаходять яку-небудь її первісну, а потім складають різниця значень цієї первісної при верхній і нижній межах інтегрування.
Наприклад: 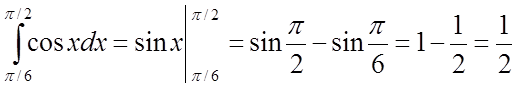 .
.
Очевидно, усі методи обчислення невизначених інтегралів можуть бути безпосередньо застосовані і до обчислення визначених інтегралів, при цьому самі обчислення в багатьох випадках значно спрощуються в порівнянні з обчисленнями, виробленими по загальному методі.
Метод підстановки
Якщо під знаком
інтеграла стоїть складна функція ![]() і поруч стоїть похідна
складного аргументу
і поруч стоїть похідна
складного аргументу ![]() , тобто маємо
, тобто маємо
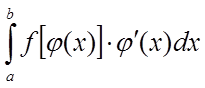 ,
,
тоді робимо підстановку ![]() подібно тому, як робили це в невизначеному
інтегралі, але знаходимо нові межі інтегрування, і тоді не потрібно повертатися
до початкового перемінного.
подібно тому, як робили це в невизначеному
інтегралі, але знаходимо нові межі інтегрування, і тоді не потрібно повертатися
до початкового перемінного.
Наприклад: 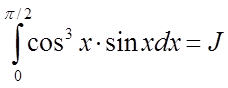 .
.
Робимо
підстановку: 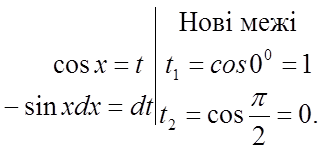
Підставляємо в даний інтеграл:
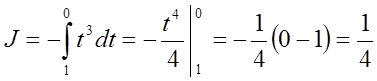 .
.
Метод інтегрування вроздріб
Теорема. Нехай функції u(х) і
v(х), задані на відрізку ![]() , мають там безперервні
похідні, тоді
, мають там безперервні
похідні, тоді
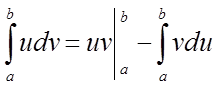 .
.
Наприклад: 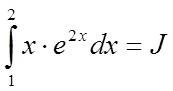 .
.
Покладемо
![]()
![]()
![]()
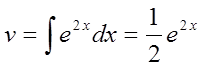
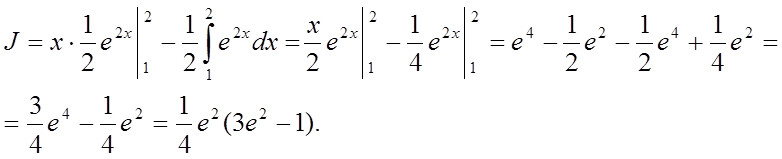
3. Невласні інтеграли.
Визначений
інтеграл 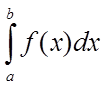 , де проміжок інтегрування
, де проміжок інтегрування ![]() кінцевий, а підінтегральна функція
кінцевий, а підінтегральна функція ![]() безперервна на відрізку
безперервна на відрізку ![]() , називають ще власним інтегралом.
, називають ще власним інтегралом.
Розглянемо так називані невласні інтеграли, тобто визначені інтеграли від безперервної функції, але з нескінченним проміжком інтегрування, або визначений інтеграл з кінцевим проміжком інтегрування, але від функції, що має на ньому нескінченний розрив.
Нехай функція ![]() безперервна на проміжку
безперервна на проміжку ![]() . Якщо існує кінцева межа
. Якщо існує кінцева межа 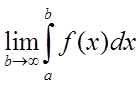 , то його називають невласним інтегралом
першого роду і позначають
, то його називають невласним інтегралом
першого роду і позначають 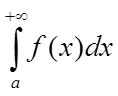 , у такий спосіб
, у такий спосіб
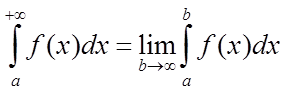 .
.
У цьому випадку
говорять, що невласний інтеграл 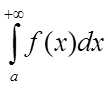 збігається.
збігається.
Якщо ж зазначена
межа не існує або він нескінченний, то говорять, що інтеграл 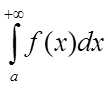 розбігається.
розбігається.
Аналогічно
визначається невласний інтеграл на проміжку ![]() :
:
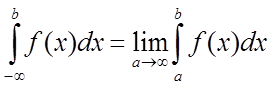 .
.
Невласний інтеграл із двома нескінченними межами визначається формулою:
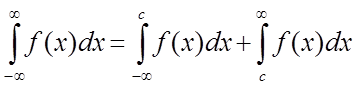 ,
,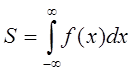
де с – довільне число.
Інтеграл, що стоїть в лівій частині рівності, буде збігатися лише тоді, коли збігаються обидва інтеграли праворуч.
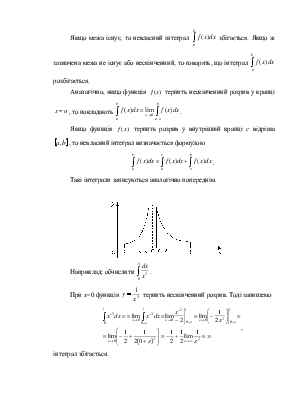
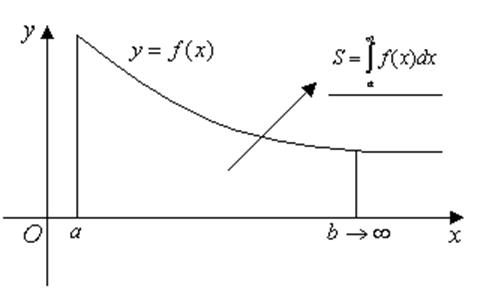
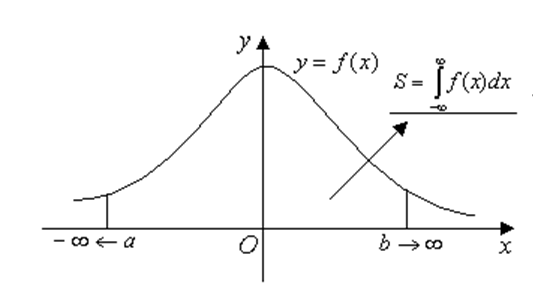
З геометричної точки зору інтеграли, що збігаються, з нескінченними межами можна розглядати (відповідно) як площі «нескінченних трапецій»:
Приклади.
1) 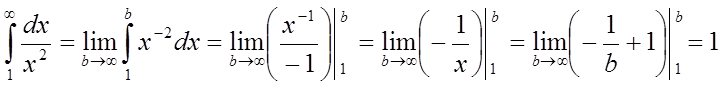 ,
,
тобто інтеграл збігається.
 |
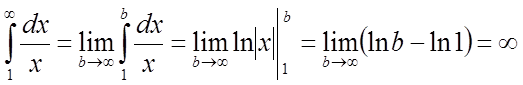 ,
тобто інтеграл розбігається.
,
тобто інтеграл розбігається.
 |
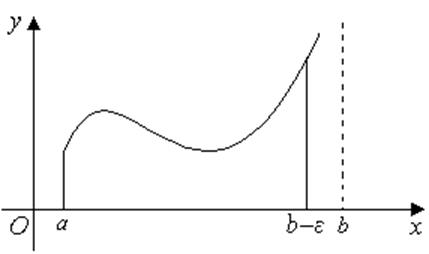 |
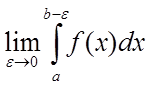 ,
то його називають невласним інтегралом другого роду і позначають
,
то його називають невласним інтегралом другого роду і позначають 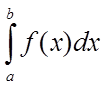 , тобто
, тобто 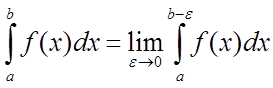 .
.
Якщо межа існує,
то невласний інтеграл 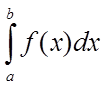 збігається. Якщо ж
зазначена межа не існує або нескінченний, то говорять, що інтеграл
збігається. Якщо ж
зазначена межа не існує або нескінченний, то говорять, що інтеграл 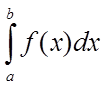 розбігається.
розбігається.
Аналогічно, якщо
функція ![]() терпить нескінченний розрив у крапці
терпить нескінченний розрив у крапці ![]() , то покладають
, то покладають 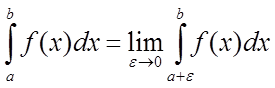 .
.
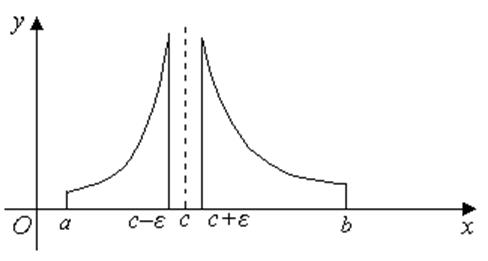
Якщо функція ![]() терпить розрив у внутрішній крапці с
відрізка
терпить розрив у внутрішній крапці с
відрізка ![]() , то невласний інтеграл визначається
формулою
, то невласний інтеграл визначається
формулою
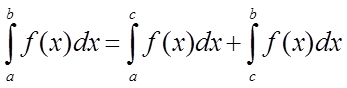 .
.
 |
Наприклад:
обчислити 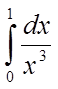 .
.
При х=0
функція 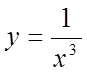 терпить нескінченний розрив. Тоді запишемо
терпить нескінченний розрив. Тоді запишемо
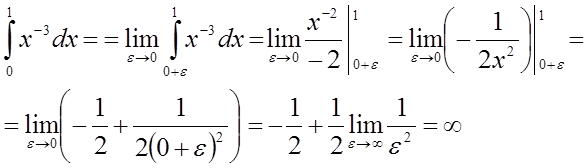 ,
,
інтеграл збігається.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.