Составление портфеля из разновидностей ценных бумаг. Составление портфеля из рискового и безрискового активов. Спрос на деньги в теории портфеля

Лекция 9.

1.Составление портфеля из п разновидностей ценных бумаг

Для определения области выбора инвестора при составлении портфеля из любого числа разновидностей рисковых активов поступим следующим образом. Оптимальный портфель, составленный из двух пакетов акций  и , будем рассматривать в качестве одной из разновидностей ценных бумаг  с ожидаемой доходностью  и риском . По правилам, изложенным в предыдущем разделе, составим оптимальный портфель из ценной бумаги  и третьей акции . Полученный в результате этого портфель будем рассматривать как ценную бумагу  с ожидаемой доходностью  и риском . Присоединив к ней четвертую акцию , составим оптимальный портфель  и т. д.

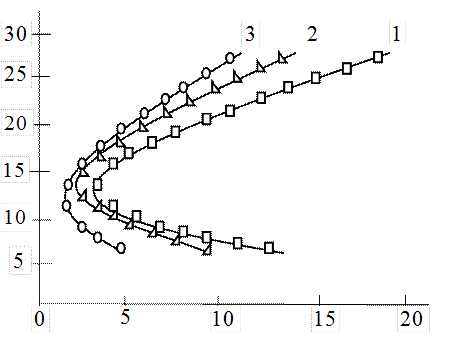
Рис. 1.1. Область выбора инвестора при составлении портфеля из четырех разновидностей акций.

Акции: 1 - , 2 - , 3 - .

Рис. 1.1 иллюстрирует зависимость доходности составляемого таким образом портфеля от его риска. Линия 1 — это множество всевозможных комбинаций ,  портфеля из акций  (, ) и  (, ) при , изображенная на рис. 1.2 в квадранте I. Минимальным риском обладает портфель , в котором имеется 78% акций  и 22% акций . Линия 2 представляет всевозможные сочетания ,  портфеля, содержащего портфель  с минимальным риском, т.е. 78% акций  и 22% акций , и акцию  (, ), доходность которой не зависит от доходности акций  и . Портфель , содержащий 86% портфеля  и 14% акаций , соответствует точке перегиба линии 2, т.е. обладает минимальным риском. Линия 3 есть совокупность всевозможных комбинаций ,  портфеля, образованного из портфеля , и еще одной акции  c  и . Продолжая таким образом составлять портфели из  разновидностей ценных бумаг, получим область выбора в пространстве ,  в виде заштрихованной фигуры, изображенной на рис. 1.2.

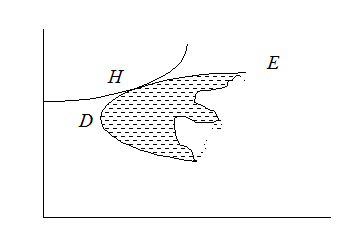
Рис. 1.2. Оптимальный портфель, составленный из  разновидностей акций.

Однако эффективная область выбора для инвестора, не склонного к риску, по-прежнему предстает в виде линии , ограничивающей заштрихованную площадь сверху, так как все другие точки площади представляют менее предпочтительные портфели либо по доходности, либо по риску, либо по доходности и риску одновременно.

Оптимальной является такая структура портфеля из  разновидностей ценных бумаг, которая максимизирует функцию полезности инвестора: . Графически она определяется точкой касания наиболее отдаленной кривой безразличия с верхней границей площади выбора (точка  на рис. 1.2).

2.  Составление портфеля из рискового и безрискового активов

Проследим за поведением инвестора в условиях, когда формирование портфеля из  разновидностей рисковых акций сочетается с возможностью ссужать и занимать деньги по единой гарантированной ставке процента. Обозначим долю средств инвестора, которую он затратил для приобретения рисковых активов ; тогда доля, используемая на денежном рынке, равна . Так как инвестор может занять деньги для увеличения портфеля, то  может быть больше 1, а . Вычислим ожидаемую доходность всех финансовых средств  инвестора в соответствии с формулой (Лекция 5.1.3):

.

Риск ожидаемой доходности определяется только риском портфеля, т.е. 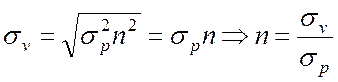. Оба параметра —  и  являются линейными функциями от доли рискового портфеля в общем объеме финансовых средств. Поэтому между ними тоже существует линейная зависимость:

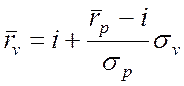.                                                       (2.1)

 

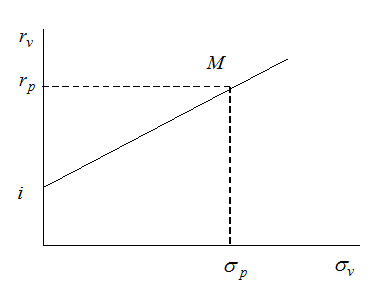
Рис. 2.1. Область выбора при составлении портфеля из рисковых и безрисковых активов.

          Графически эта зависимость представлена на рис. 2.1 прямой, пересекающей ось ординат в значении . Она представляет область выбора для инвестора в условиях совместного существования рынка рисковых ценных бумаг и совершенного рынка денег. Каждый субъект выбирает на прямой  точку в соответствии со своей функцией полезности, т.е. точку касания этой прямой с наиболее отдаленной кривой безразличия. Выбор точки  означает, что все свои средства инвестор вложил в рисковые активы. Все точки, расположенные левее , соответствуют определенному распределению средств между акциями и денежной ссудой. Точки, расположенные правее , представляют имущество, состоящее из портфеля ценных бумаг и денежной задолженности инвестора.

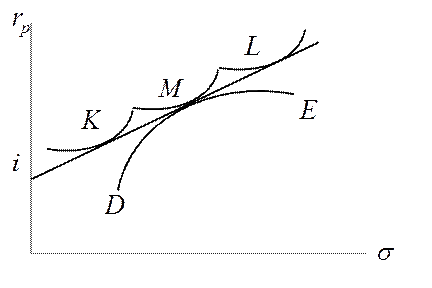
Рис. 2.2. Оптимальный портфель из рисковых и безрисковых активов.

Обратимся теперь снова к эффективному множеству портфелей, содержащих  рисковых ценных бумаг, — к линии , воспроизведенной на рис. 2.2. На этой линии можно выделить примечательную точку — точку касания с прямой, проведенной через точку  на оси ординат. Поскольку при существовании совершенного денежного рынка областью выбора инвестора является прямая, пересекающая ось ординат в точке , то в этих условиях множество эффективных портфелей рисковых активов превращается в точку . Любой точке на кривой , кроме точки , соответствует более эффективная точка на прямой, проходящей через точку , при том же уровне риска достигается большая доходность финансовых вложений.