Рішення диференціальних рівнянь вищих порядків (рівняння вищих порядків, що припускають зниження порядку)і: Практичне заняття № 3

Практичне заняття №3.

“Рішення диференціальних рівнянь вищих порядків

(рівняння вищих порядків, що припускають зниження порядку)”

I. Рівняння вищих порядків, що припускають зниження порядку

Розглянемо деякі види диференціальних рівнянь, що допускають зниження порядку:

1.       .                                                                                  (1)

Після n-кратного інтегрування одержуємо загальне рішення:

.

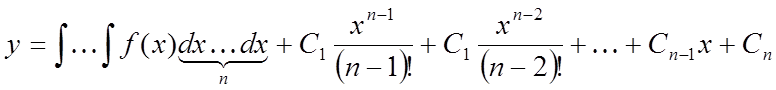2.       Рівняння другого порядку, що не містять явно функції у:

.                                 (2)

Порядок рівняння можна понизити заміною перемінної:

,

,

тоді рівняння (2) стане рівнянням першого порядку одного з раніше розглянутих видів. Після того, як ми знайшли рішення рівняння

підставляємо замість ρ похідну у', інтегруємо ще раз і одержуємо загальне рішення вихідного рівняння (2):

.

3.       Рівняння другого порядку, що не містять явно незалежного перемінного:

.                                 (3)

знижуємо також порядок похідної введенням нової функції

,

причому ρ розглядається як залежна від у, тобто

,

.

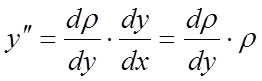Після підстановки у' і у'' у рівняння (3), інтегруючи його, підстановки замість ρ похідній у' і повторного інтегрування одержимо загальне рішення рівняння (3).

Приклад 1.

Знайти загальне рішення рівняння .

Рішення.

Інтегруючи послідовно дане рівняння три рази, одержимо:

,

,

.

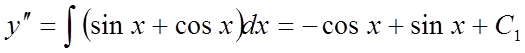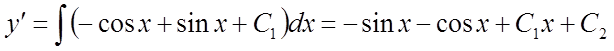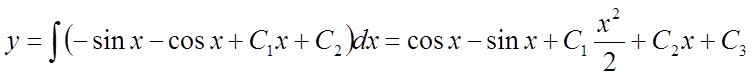Приклад 2.

Знайти загальне рішення рівняння

.

Рішення.

Знижуємо порядок похідної, позначаючи , , одержимо рівняння першого порядку:

.

Розділяємо перемінні

,

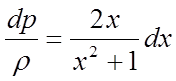інтегруємо і записуємо загальне рішення рівняння

.

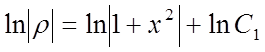
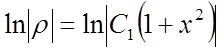
Підставляємо замість  і ще раз інтегруємо

,

,

 

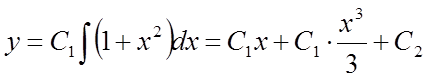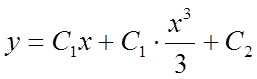
– загальне рішення рівняння.

Приклад 3.

Знайти загальне рішення рівняння

.

Рішення.

Рівняння не містить явно незалежного перемінного.

Знижуємо порядок похідної, позначаючи , тоді:

.

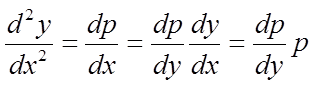Перетворене диференціальне рівняння буде мати вигляд:

,

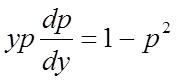інтегруємо і записуємо загальне рішення рівняння

,                 ,

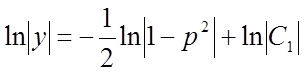
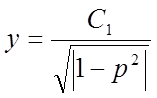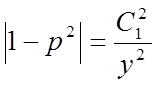тобто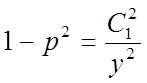, або , або .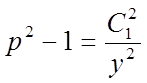

В першому випадку:

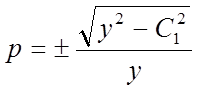  або    ;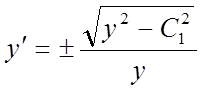

розділення перемінних дає нам:

,

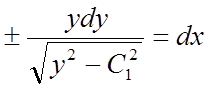й інтегруванням отримаємо:

.

          Звідси

.

В другому випадку:

;

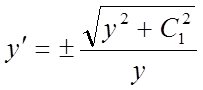розділення перемінних дає нам:

,

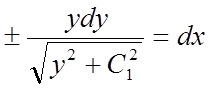й інтегруванням отримаємо:

.

          Звідси

.

Обидва випадки можна об'єднати в одній формі:

–  загальне рішення рівняння.

Приклад 4.

Знайти загальне рішення рівняння

.

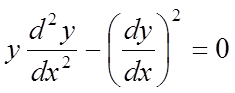Рішення.

Рівняння не містить явно незалежного перемінного.

Знижуємо порядок похідної, позначаючи 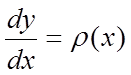, , 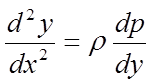одержимо рівняння першого порядку:

.

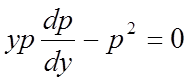Розділяємо перемінні

,

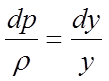інтегруємо і записуємо загальне рішення рівняння

,

,

,

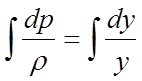               або                 .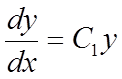

Підставляємо замість  і ще раз інтегруючи, отримаємо:

,

 .

– загальне рішення рівняння.