Степеневі ряди. Радіус і коло збіжності. Теорема Абеля. Степеневі ряди Тейлора та Маклорена. Застосування рядів до наближених обчислень

Лекція 5

План.

1.  Степеневі ряди. Радіус і коло збіжності. Теорема Абеля.

2.  Степеневі ряди Тейлора та Маклорена.

3.  Застосування рядів до наближених обчислень

1. Степеневі ряди

Визначення. Степеневим  рядом називається функціональний ряд

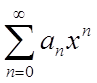,                                              (1)

де a_n – числа.

Теорема Абеля

1.  Якщо степеневий  ряд (1) збігається при , то він абсолютно збігається при всякому значенні х, для якого .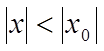

2.  Якщо ряд розбігається при деякому значенні , то він розбігається при всякому х, для якого .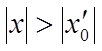

Доказ.

1.  При х=х₀ збігається числовий ряд 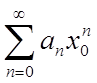, тоді з необхідності ознаки випливає 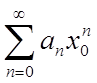 при . Це значить, що існує таке позитивне число М, що всі члени ряду по модулю менше М. Перепишемо ряд (1)

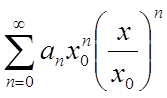                                               (2)

Оцінимо ряд (2), узявши його члени по абсолютній величині

.

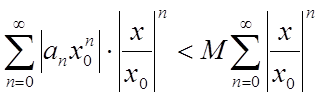При 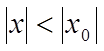 останній ряд збігається як сума убутної геометричної прогресії. Отже, збігається і ряд, складений з абсолютних величин, а це значить, що ряд (2) або (1) збігається абсолютно.

2.  Нехай ряд (1) розбігається в крапці , тоді він буде розбігатись в будь-якій крапці х, що задовольняє умові 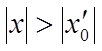. Якщо ряд збігається, то в силу частини 1 теореми він збігався б у крапці . Але це суперечить умові, що в крапці  ряд розбігається. Отже, ряд розбігається в крапці х. Що і було потрібно довести.

Обчислення радіуса збіжності степеневого ряду

Визначення. Інтервалом збіжності степеневого ряду називається такий інтервал , що для всякої крапки х, що лежить усередині нього, ряд збігається і притім абсолютно, а для крапок х, що лежать поза ним, ряд розбігається. Число R називається радіусом збіжності степеневого ряду. На кінцях інтервалу  питання про збіжність або розбіжність вирішується індивідуально для кожного конкретного ряду.

Теорема. Нехай даний степеневий ряд 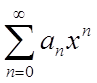 (1) і існує кінцева межа .

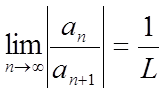1.  Тоді радіус збіжності степеневого ряду

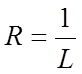, якщо .

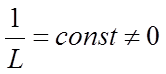2.  , якщо .

3.  , якщо .

Доказ.

Розглянемо ряд з абсолютних величин членів ряду (1) 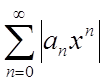 і будемо вважати, що він збігається на деякому проміжку числової осі. Визначимо цей проміжок. Для цього скористаємося ознакою Даламбера.

.

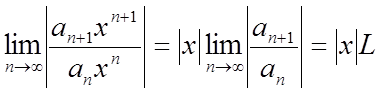Отже, ряд (1) збігається абсолютно при 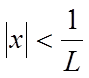, розбігається при  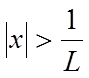на підставі необхідної ознаки збіжності.

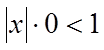Якщо , то з нерівності  випливає, що ряд (1) збігається на всій числовій осі, тобто .

Якщо , то степеневий ряд збігається в одній єдиній крапці х=0, тобто .

Наприклад: даний ряд 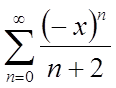. Визначити радіус збіжності і досліджувати його на кінцях інтервалу.

;                    

.

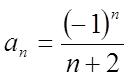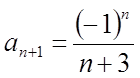
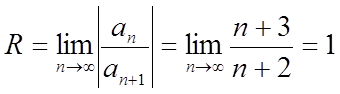В інтервалі (–1, 1) ряд збігається абсолютно, поза інтервалом розбігається.

1.  Нехай х = –1 (підставимо в степеневий ряд).

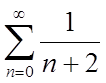 – розбігається як гармонійний ряд.

2.  х = 1,           .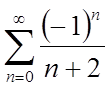

1)

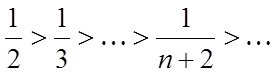
2) .

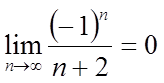По ознаці Лейбница ряд збігається. Складемо ряд з абсолютних величин даного ряду й одержимо гармонійний ряд, що розбігається. Тобто при х = 1 ряд збігається умовно.

Теорема. Якщо степеневий ряд має інтервал збіжності , то ряд, отриманий його почленним диференціюванням, має той же інтервал збіжності.

2. Степеневі ряди Тейлора і Маклорена

Для функції , що має всі похідні до  порядку включно, в області крапки  справедлива формула Тейлора

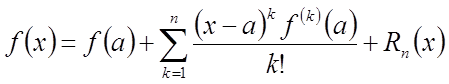,                          (3)

де залишковий член обчислюється по формулі

;           .

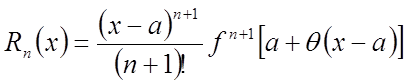Якщо має похідні всіх порядків в околиці крапки , то у формулі Тейлора число n можна вибрати як завгодно великим. Нехай у розглянутій околиці

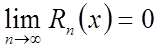.                                     (4)

Тоді, переходячи в (5) до межі при , одержимо нескінченний ряд, що називається рядом  Тейлора:

.

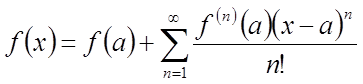Якщо в ряді Тейлора покласти , то одержимо окремий випадок, що називається рядом Маклорена

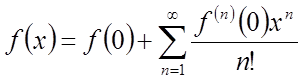                                      (5)

Приклади розкладання елементарних функцій у ряди Маклорена:

1)   .

.

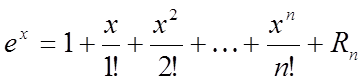
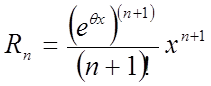Значення х розглядається в околиці крапки 0. Тобто R_n є відношення обмеженої величини і нескінченно великий і справедливо (4). Значить  можна представити рядом Маклорена

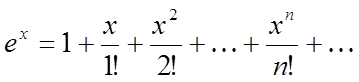                              (6)

Ряд (6) збігається абсолютно до функції  на всій числовій осі.

2)  .

Складемо формулу Маклорена для

.

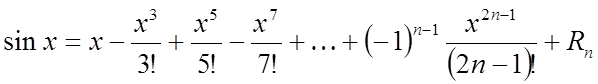
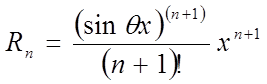Аналогічно пунктові 1, переконуємося в справедливості (4). Отже, функція розкладається по формулі (5).

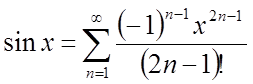.                                            (7)

3) 

Про диференціюємо ряд (7) почленно, одержимо знову що абсолютно збігається на всій числовій осі ряд Маклорена для функції

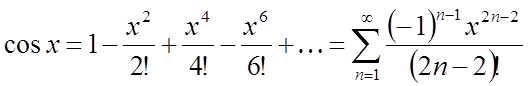.                    (8)

3. Застосування рядів до наближених обчислень

Для обчислення наближених значень функції з заданою точністю зручно користуватися рядами в тому випадку, коли відповідний ряд є знакочергуючимся. Для знакочергуючогося ряду, що збігається, легко оцінити погрішність наближеного значення суми - вона менше абсолютного значення першого з відкинутих членів.

Наприклад, візьмемо ряд для функції :

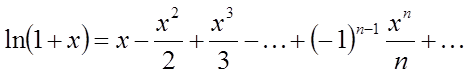, що збігається до  в інтервалі (–1, 1) і, думаючи ; одержимо ряд для обчислення  з будь-якою точністю:

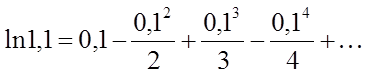
Абсолютне значення четвертого члена цього ряду менше 0,0001, тому, відповідно до властивості знакоперемінного ряду, для обчислення наближеного значення  з точністю 0,0001 досить узяти суму трьох перших членів ряду:

.

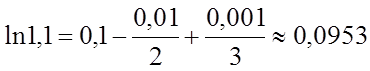За допомогою рядів можна обчислювати наближені значення інтегралів, що не беруться в кінцевому виді.

Наприклад: обчислити з точністю до 0,0001 наближене значення інтеграла .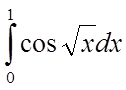

Скористаємося рядом Маклорена для , заміняючи в ньому х на , маємо:

    .

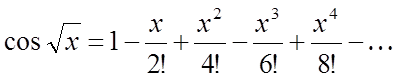
Інтегруючи в зазначених межах, одержимо

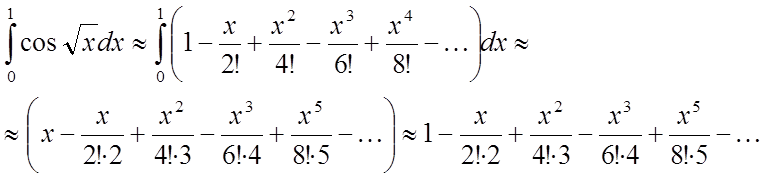
П'ятий член цього знакочергуючогося ряду, що збігається, менше 0,0001. Тому для обчислення шуканого наближеного значення інтеграла досить узяти суму чотирьох перших членів ряду:

.

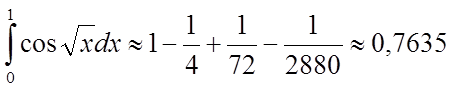За допомогою рядів можна вирішувати також диференціальні рівняння.